

The set of circles tangent to two given circles provides a very rich problem environment. The following investigations are my attempt to discover more about tangent circles. I look at a few possible areas of related problems and exploration and discover that the base of the key isosceles traingle in each construction is the secret to the construction. I set my 2 given circles to be green. The tangent circle is either blue or red.
Basically, the steps to construct the tangent can be summarized as follows.
1. Given 2 circles, such that circle 1 lies within circle 2 i.e. Circle 2 is the bigger circle.
2. Put a point A on the circle2.
3. Using A as the center, construct circle 3 with radius of circle 1
4. Connect center of circle 1 with center of circle 3
5. Connect center of circle 1 with circle 3 (the part that lies outside circle 2)
6. Construct the perpendicular bisector for step 5. We obtain the center of the tangent circle.
7. Radius of the tangent circle is the distance from center of circle 3 to the point constructed in 6.
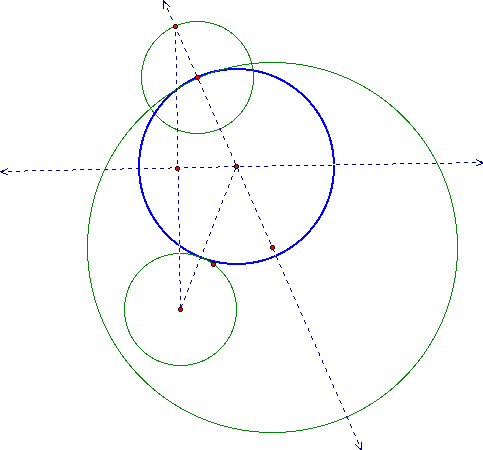
The script tool for the above tangent circle can be found in my assignment 5. When I trace the center of the tangent circle, an ellipse is obtained with foci at the centers of the 2 given circles. This sum is a constant and this explains why the centers of the tangent circles is an ellipse with foci at the centers of the given circle.
Loci of the centers of tangent circles in the above tangent circle (Figure 2) gives an ellipse.
Proof
MP = MN + NP and F1M=MP
F2M+MP is a constant as seen from the constrcution above.
And, we see clearly from above,
F2M + MP
=F1M + F2M
= sum of distance from the 2 foci of ellipse to the same point of the ellipse (This is the property for an ellipse)
= radius of the 2 green circles
= constant
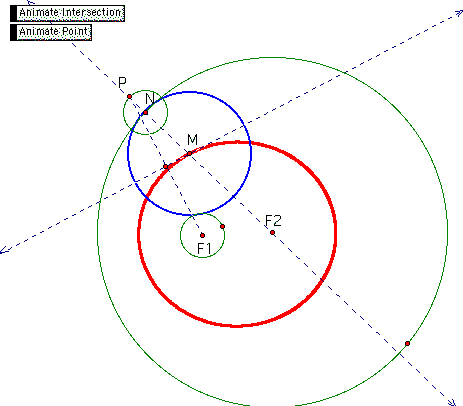
Problem 2
Given 2 green circles, we put a point N on the bigger green circle. The 2 green circles are fixed. We obtain different tangent circles as we move N along the bigger green circle. Loci of the center of the tangent circle is an ellipse.
Problem 3a
Next, I construct the tangent circle to two given circles. The given point is on the smaller of the two circles so that the smaller circle is external to the tangent circle.
Loci of the center of the tangent circle is an ellipse.
Problem 3b
I construct the tangent circle to two given circles. The given point is on the smaller of the two circles so that the smaller circle is internal to the tangent circle.
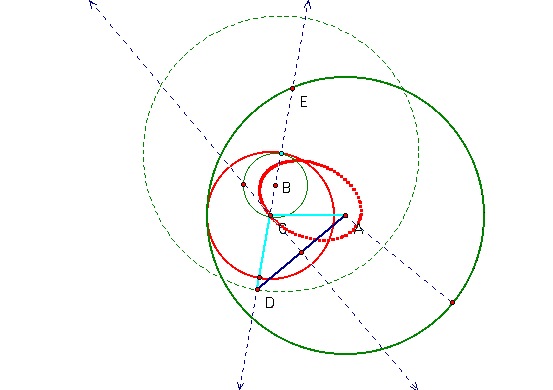
Loci of the center of the tangent circle is an ellipse.
Question 5
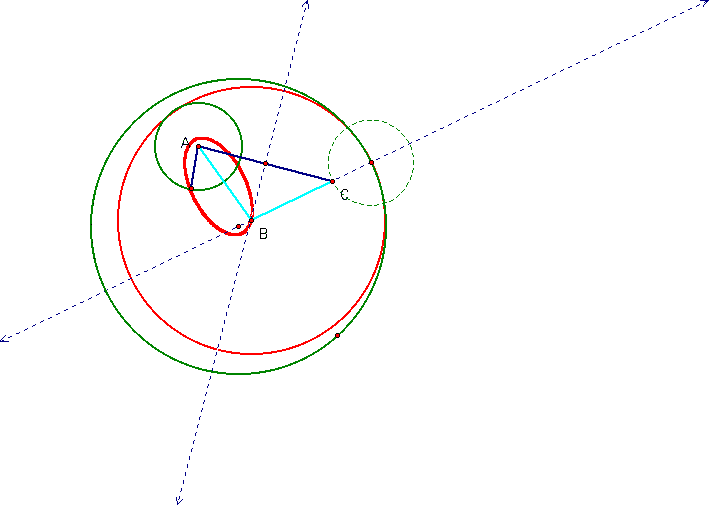
I would like to discuss how I construct the following tangent circles (Figure 6) when the two given circles intersect. The given point is on the bigger of the two circles. I know that the foci of the ellipse formed by the locus of the tangent circle are at the centres of the 2 given circle The center of the tangent circle will also lie along a line from the center of the given circles with the specified point on the bigger green circle. I constructed an additional circle (dotted green circle) with radius the same as the smaller circle with center at the designated tangent point. Connect the center of the additional circle and center of the bigger green circle. We call this line CE. Construct a segment through the center of smaller green circle and point C as shown in the diagram below. This segment is the base of the isosceles triangle. Bisect this segment. The perpendicular bisector is always tangent to the ellipse formed by the trace of the center of the tangent circle. The intersection bewteen the perpendicualr bisector and line CE gives the center of the tangent circle O. Lastly, we construct our tangent circle with center O and radius OF.
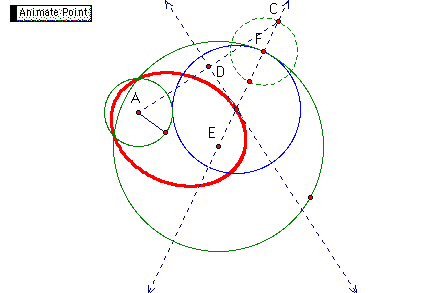
Question 6
The locus of the centers of the constructed tangent circles when the two circles intersect is an ellipse. From Figure 6, it is esay to see and explain why the trace is an ellipse. using the property of a perpendicular bisector, AO = OC where O is the center of the tangent circle. OE + OC = OE+AO is always a constant by our construction. (because this segment is always of length the sum of the radius of the desired circle plus radius of the given circle with center F). We note that OE + OA = constant = the property of an ellipse. Hence, the observable trace is an ellipse.
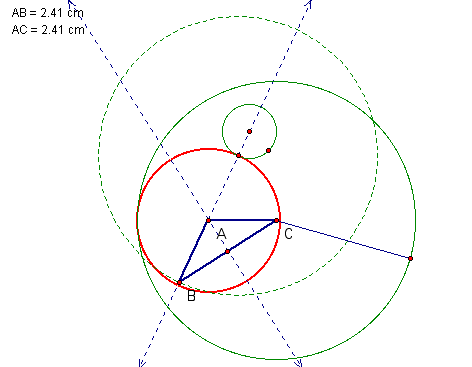
Question 8

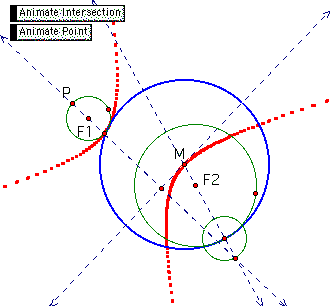
Figure 7 is the result of the construction of circles tangent to 2 different disjoint circles. We want to show that the locus of the center is the hyperbola with foci at the centers of the 2 given circles.
The above hyperbola is formed because
![]() = constant=radius of the 2 green
circles = property of a hyperbola.
= constant=radius of the 2 green
circles = property of a hyperbola.
Question 9
When I trace the line tangent to the ellipse, as the constructed circle moves around the large circle, I observe an envelop of lines tangent to the ellipse.The trace of the tangent line in each case gives a hyperbola. As the 2 given circles approach being tangent, the trace seems to be an ellipse.


Question 10
Next, I look at the locus of the midpoint of the segment that formed the base of the key isosceles triangle in each of my construction. The locus of the midpoint of the segment that formed the base of the key isosceles triangle in each construction is a circle. When the two given circles re tangent to one another, the diameter of the tangent circle connects the centers of the 2 given circles.
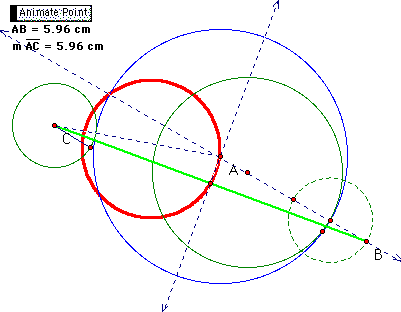
My investigation on tangent circles end here. I enjoy assignment 7 and learnt a great deal from the above investigation because it took me a very long time(but meangingful and well-spent) to figure out the above constructions and underlying meaning behind each construction. I would like to thank Bob and Steve for their encouragement as I struggle with this assignment for some time.