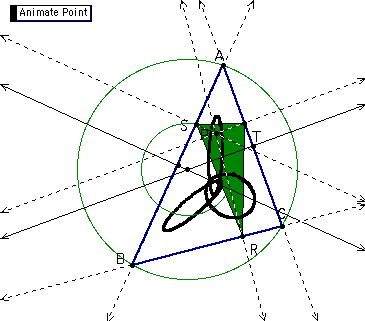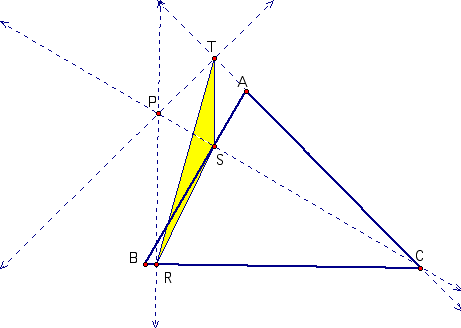
ABC is any triangle. P is any point in the plane. Triangle RST is known as the pedal triangle and it is formed by constructing perpendiculars to the sides of ABC. The GSP script tool for the general construction of a pedal triangle to traingle BC where P is any point in the plane ABC can be found in my assignment 5.
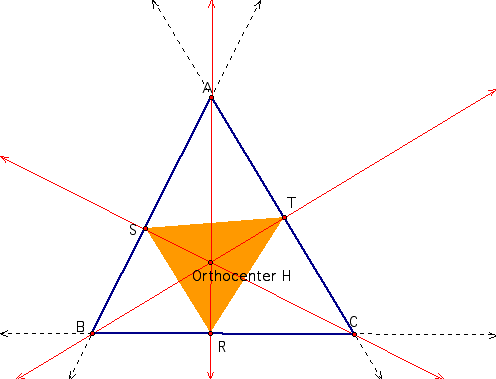
If the pedal point P is the centroid or orthocenter of triangle ABC, the area of the pedal triangle is equal to 4 and less than a quarter of the area of ABC respectively. The centroid always lies inside triangle ABC. If P is the orthocenter H of triangle ABC then we obtain a special pedal triangle called the orthic triangle. The orthic triangle partitions the original triangle into three additional triangles each of which is similiar to the original triangle.
Proof
We want to show that ABC is similar to STA.
Quadrilateral BSTC is cyclic beacuse BST and STC are right angles.
SBC is supplementary to STC.
STA is supplementary to STC.
Hence, SBC is similiar to STA because both triangles share SAT.
We repeat the procedure to show ABC is similiar to BSR and ABC is similar to RCT.
The altitudes AR, CS and BT are concurrent.
Proof
ASC is similar to ATB and
BRA is similar to BSC and
CTB is similar to CRA and
Multiply (A), (B), (C), we have
When P is inside ABC, on altitude AR,
Then,
Also, when P is the orthocenter,
We want to proof:
From figure 1,
(1) implies
(2) implies that
Hence,
The proofs are similar for the 2 equations below.
![]()
![]()
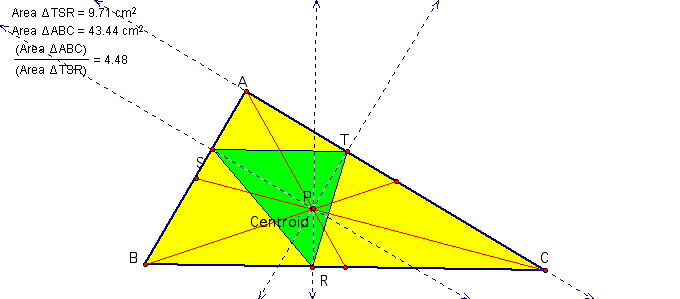
We notice that the area of the pedal triangle is exactly one quarter of the area of triangle ABC if P is at the circumcenter of triangle ABC. This is true even if the circumcenter C is outside ABC.
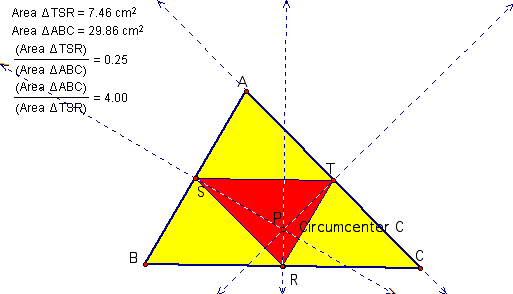
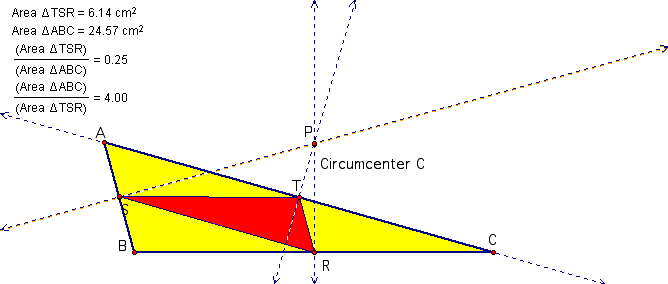
When P lies on the circumcircle of ABC, I notice that points RST becomes collinear. This line segment is called the Simson line. We set the path of the pedal point be the circumcircle. When the Simson line is traced as the pedal triangle moves along the circumcircle, the envelop of the Simson line seems to look like a trapped triangle in the circumcircle.
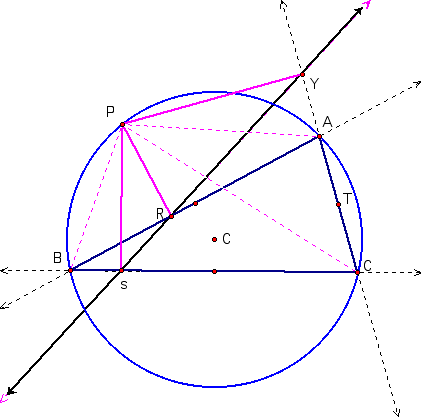
Proof that Simson line SRY is collinear.
Given P is on the circumcircle. PYA is supplementary to PRA and both are right angles. PRAY is cyclic so their opposite angles are supplementary. Angle PYR is the same as angle PAR as both are inscribed in the same arc. PYC is supplementary to PSC and both are right angles. Quadrilateral PSCY is cyclic so their opposite angles are supplementary. Angle PYS is the same as angle PCB as both are inscribed in the same arc. By law of transitivity, angle PYR is the same as angle PYS. since PYR and PYS share the same ray YP, YR and YS must coincide. Hence SRY are collinear.
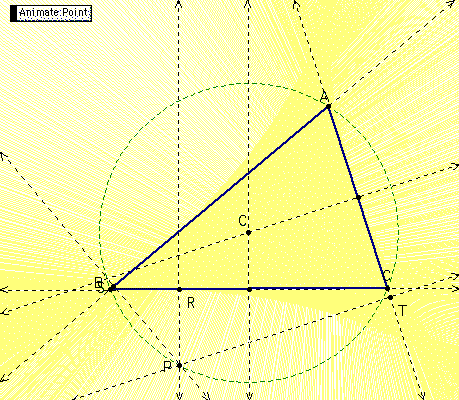
Next, I locate the midpoints of the sides of the Pedal triangle. I constructed a circle with center at the circumcenter of triangle ABC such that the radius is larger than the radius of the circumcircle.
The locus of the midpoints of the sides of the pedal triangle is traced as Pedal Point P is animated around the circle that I have constructed. When the radius of the constructed circle is bigger than the radius of the circumcircle, I obtain 3 interlocked rings.
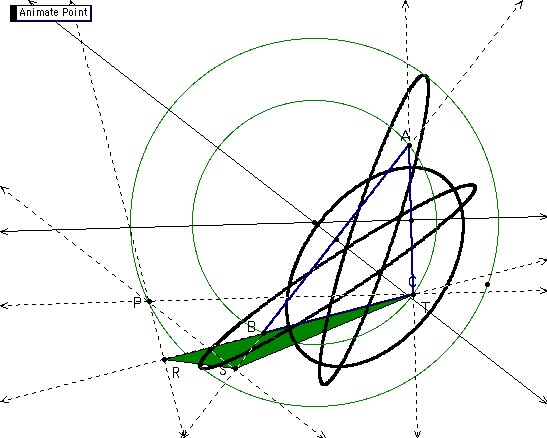
When the radius of the constructed circle is smaller than the radius of the circumcircle, the follwing trace (3 interlocked rings) is observed.