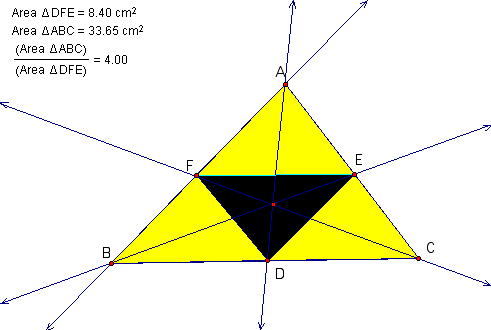
In traingle ABC below, a point P inside the triangle is selected. Lines AP, BP and CP are extended to their intersections with the opposite sides in points D,E and F respectively.
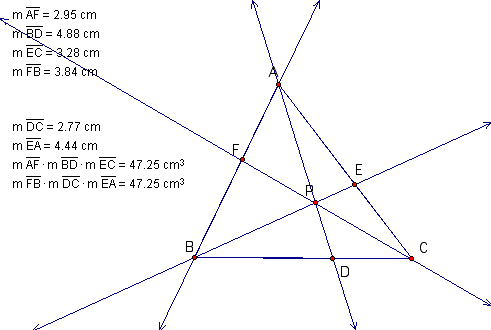
(AF)(BD)(EC) also have the same measurement as (FB)(DC)(EA) for various triangles and various locations of P. Hence,
Three lines drawn from the vertices A,B and c of ABC meeting opposite sides in points D, E and F respectively are concurrent iff
the above theorm is Ceva's theorem.
Proof:
Draw a line through A, parallel to BC meeting CP at S and BP at R.
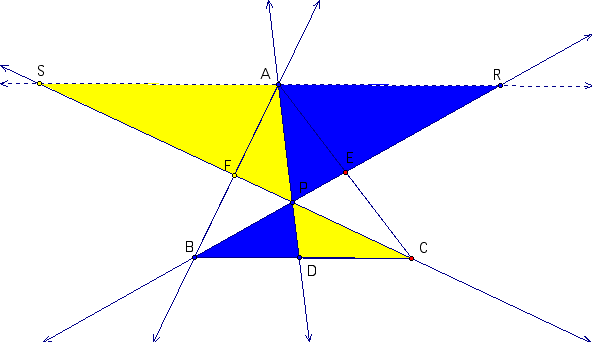
AER is similar to CEB. Therefore
BFC is similar to AFS. Therefore
CDP is similar to SAP. Therefore
Therefore,
(3) and (4) gives
Multiply (1), (2) and (5) gives
We now prove that DEF are concurrent.
Given ABC with F on AB, E on AC and D on BC. Also
We now show that AD, BE and CF are concurrent. let BE and AD meet at P. Let CP meet AB at N. Since AD, BE and CN' are concurrent, by part of Ceva's theorem, we have
But given
Hence, it is clear that
So, N' and F must coincide. Hence the 3 lines are concurrent.
When P is inside the triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4.
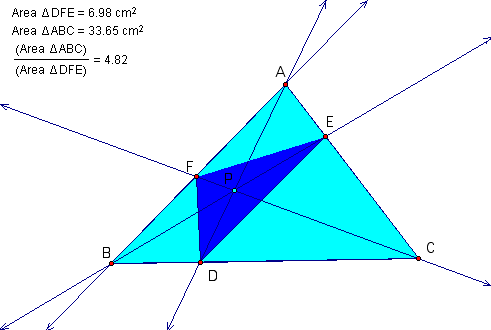
The ratio is exactly four when P is at the centroid of ABC. We have proven earlier in Assignment 4 that Area FED is 1/4 area of ABC.
Through observation, the largest possible area of FED is 1/4 area of ABC.
Maximum Area of FED = 1/2 (DE)(FH) = 1/2(1/2)AB(1/2)FE = 1/4 ABC
It follows that the ratio of areas ABC and DEP is always greater than or equal to 4.