Fibonacci Sequence

The Fibonnaci Sequence is a sequence of numbers developed by by an Italian mathematician by the name of Leonardo Fibonnacci. Given the first two numbers, f(0) and f(1), the other numbers are generated by adding the two preceding numbers. For example f(2)=f(0)+f(1) and f(3)=f(1)+f(2) and so on.

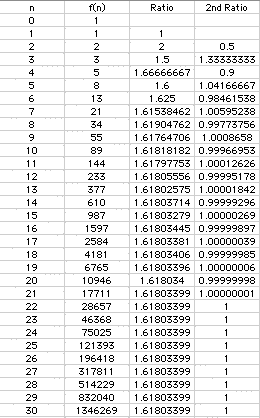
Using Microsoft Excell, I am going to explore the ratio of each pair of adjacent terms in the Fibonnaci sequence and for similar sequences. I will begin with f(0)=1 and f(1)=1.

In the chart below, let the first column be the consecative integers 0-30 and the second column be f(n). Of course the Fibonnaci Sequence goes on to infinity, but for our purposes and for the sake of time, we are going to look at f(0) through f(30). Also n cannot be less than 0 because we do not generally talk about negative numbers when discussing the nth number of a series; however f(n) can be thought of as a negative value and later we will experiment with f(n) being less than 0. Let the second column be f(n) for each intenger in the first column. Let the third column be the ratio of each number with the preceding number, i.e. f(n+1)/f(n). Also let the next column be the 2nd ratio of the f(n); therefore, each value in column 4 is the ratio of each value in column 3 with its preceding value. Click here to see the actual worksheet

From our chart we see that the ratio of the Fibonacci numbers goes to 1.61803399 as n approaches infinity and the 2nd ratio approaches 1 because each of the 1st ratios is approximately equal to the preceding value. Therefore the limit of this sequence of Fibinocci numbers is 1.6180339 as n approaches infinity.

Lets look at another sequence similar to the Fibonnaci Sequence; Again define f(n) for integer n>1 to be f(n-1)+f(n-2), but this time let f(0)=4 and f(1)=6. Click here to see the actual worksheet

Again the limit is 1.6180339 as n approaches infinity with the limit of the 2nd ratio being 1 as n approaches infinity.

Now letís look at another similar sequence know as the Lucas Sequence. Like before, the we define f(n) for integer n>1 to be f(n-1)+f(n-2), but in the Lucas Sequence f(0)=1 and f(1)=3. Click here to see the actual worksheet

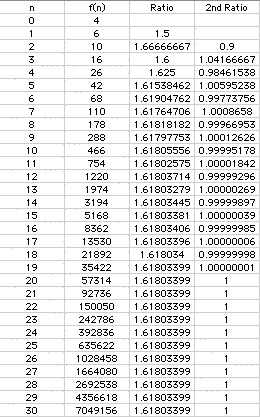
Once again the limit as n goes to infinity is 1.61803399 and the limit of the 2nd ratio as n goes to infinity is 1.

Up until now we have only discussed cases where f(n) is positive. We can now guess that the limit as n goes to infiny is 1.61803399 when f(n) is a positive number, but what if f(n) is not a positive number? Obviously f(0) and f(1) can't both because then f(n) would always be zero and our theory wonít work. But what if f(0) or f(1) were negative. Letís experiment with f(0)= -4 and f(1)=-7. Click here to see the actual worksheet

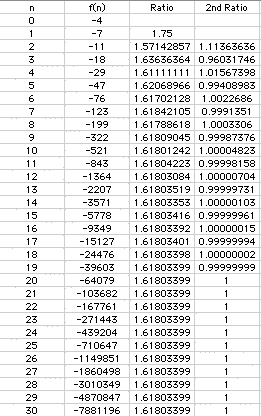
Again we come up with the same limits as before. We see that f(n) being negative does not change the results. We also see that f(1) can be less than f(0) and still work.

We now can safely assume that any sequence of numbers where f(0) and f(1) are given and both arenít equal to zero and f(n) for integer n>1 is defined as f(n-1)+f(n-2) will have a ratio whose limit is 1.61803399 and whose 2nd ratio has a limit of 1.

The value 1.61803399 is a very interesting value that is known as the Golden Ratio. It can also be expressed as [1+sqrt(5)]/2. As discussed in EMAT3500, in addition to being the limit of the sequences discussed in this problem, the Golden Ratio is found in many other real life situations. Credit cards are generally made so that the ratio of the length to the width is the Golden Ratio. The ratio of a personís height to his width is the Golden Ratio. These are only a couple of examples of where this fascinating ratio happens to occur.
The easiest way that I have found to prove that the ratios of these sequences will approach the Golden Ratio is as follows:

1. for n>1 by the definition of f(n) that we set for each sequence