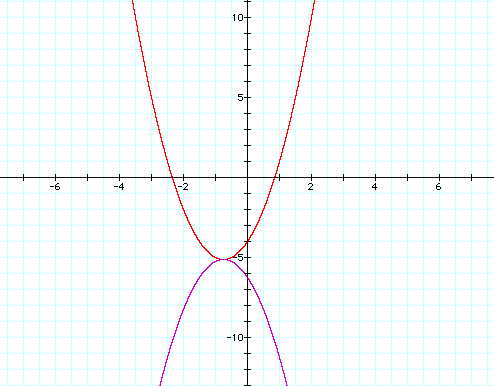
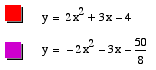The graph of this equation is a parabola with the vertex ( -3/4, -41/8 ). This vertex is located in the fourth quadrant and the graph of the equation is concave up. It can be seen that the graph is concave up because the coefficient of x^2 is positive.
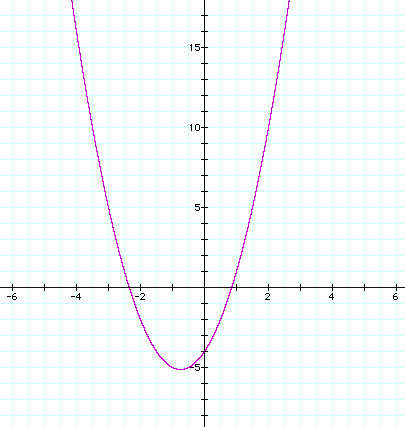
When each x is replaced by (x-4), the graph of the equation is shifted to the right four units, as demonstrated below. The vertex changes to (13/4, -41/8). The concavity and general shape of the graph, however, stay exactly the same.
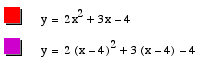
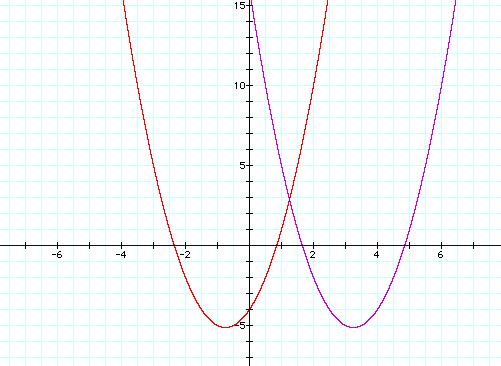
The graph can be shifted into the second quadrant by examining another form of the equation. The original equation can be written as y=2 (x+3/4)^2 - 41/8. The (x+3/4) part of the equation determines the x-coordinate of the vertex. If it is changed to (x+4), it will shift the graph further to the left. The vertical displacement, as shown in the equation above, is -41/8. This can be changed to +2 to move the graph up. The resultant graph can be seen below in the second quadrant, compared to the graph of the original equation.
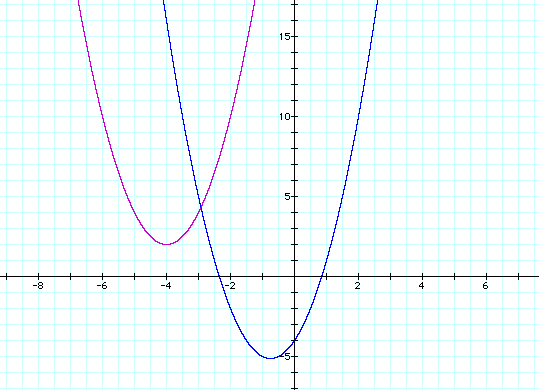
In any quadratic equation, if the coefficient of x^2 is negative, the graph is concave down. However, to keep the vertex the same and shift a graph to concave down requires more than just changing the sign of the coefficient. The sign that must actually be changed is the sign of the coefficient of the (x+a)^2 component, which in this equation is +2. When this is changed to negative 2, the items in parenthesis must be expanded and the negative sign must be applied to all components inside the parenthesis. This new equation is graphed below on the same set of axes as the original equation.