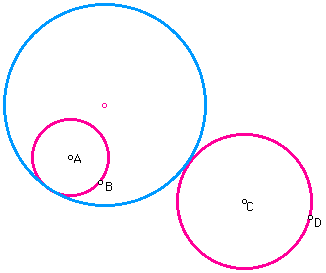
In this write up we will be looking at tangent circles. First let us look at the case that we have two circles that are outside of each other. In this case the two given circles are pink and the blue circle is tangent to both.
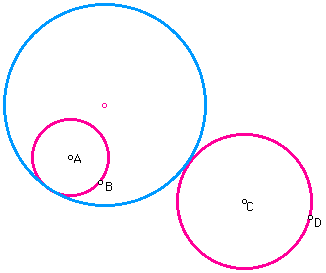
Next we will look at the case
that one of the two original circles is inside the other. Once
again, the pink circles are the originals and the blue circle
is the tangent circle.
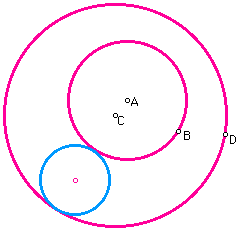
Finally we will look at the case that the two circles are overlapping. In this case the desired point of tangency makes a big difference in the location of the tangent circle. There are two pictures below. In one, the desired point of tangency on circle A is located outside circle C so the tangent circle is also outside circle C.
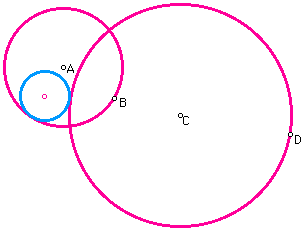
In the second case, the desired point of tangency on circle A is inside circle C therefore the tangent circle is inside of circle C and outside of circle A.
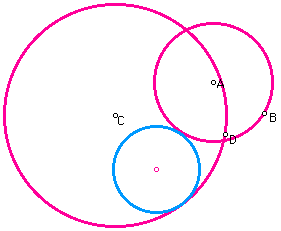
For a script to create a tangent circle to two given circles click here.