The Problem:

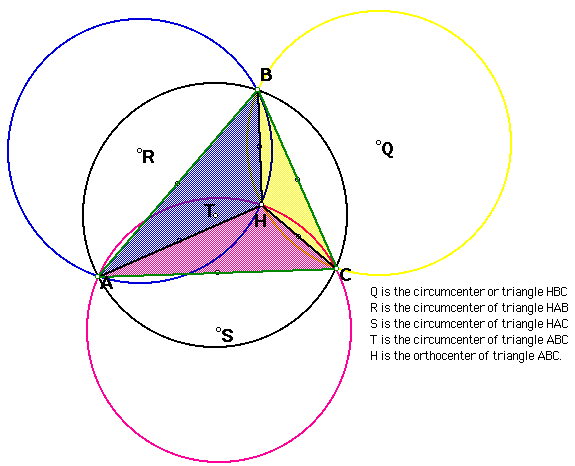
1. Construct any triangle ABC.

2. Construct the Orthocenter of triangle ABC, call it H.

3. Construct the Orthocenter of triangles HAB, HAC and HBC.

4. Construct the Circumcircles of triangles ABC,HAB, HAC and HBC.

My Conjecture:

Given any triangle ABC with orthocenter H, the circumcircle of triangle ABC is congruent to the circumcircles of triangle HAB, HAC and HBC.

The Configuration:

 

To manipulate this configurtion and observe that the four circurmcircles are always congruent, for any triangle ABC, click here.

The Proof:

 

I WILL BEGIN by proving that circle Q (the circumcircle of triangle HBC) is congruent to circle T ( the circumcircle of triangle ABC). I want to show that the segments BQ and BT (the radii of the two circles) are congruent.

Because Q is the circumcenter of triangle HBC, it lies on, j, the perpindicular bisector of segment AC (by definition).

Similarly, T is the circumcenter of triangle ABC and so it must also lie on, j, the perpindicular bisector of segment AC.

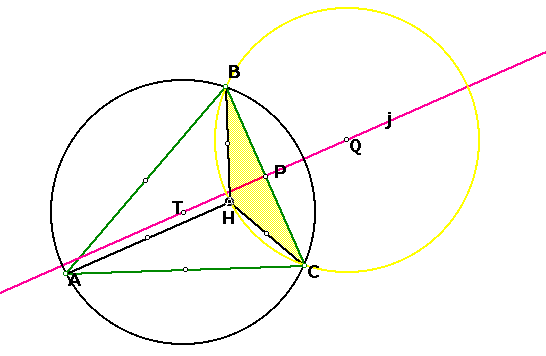
P is the point of intersection of line j and segment BC. Construct segment TQ which lies on line j, the perpindicular bisector of segment AC. Let's form four triangles: BPQ, BPT, BQC and BTC.

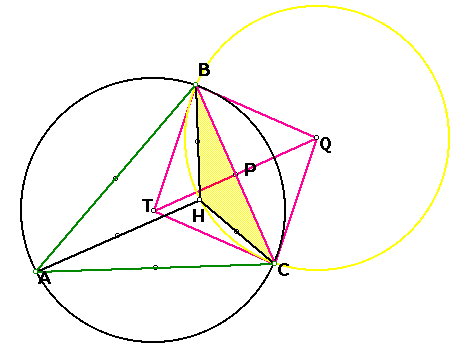
TQ is perpindicular to BC (by defn. of perp. bisector...TQ is a subset of line j).

Angle BPQ is congruent to angle BPT because they are the right angles formed by the intersection of TQ and BC.

Segment BQ is congruent to segment CQ because both BQ and CQ are radii of circle Q. Also, BT is congruent to CT because BT and CT are both radii of circle T.

Because TQ bisects AC, AP is congruent to PC (by definition of midpoint).

Therefore, triangle BQP is congruent to triangle CQP by SSS.

Since triangle BQP is congruent to triangle CQP, segment BP must be congruent to segment CP (Corresponding Parts of Congruent Triangles are Congruent).

Angle BPQ is congruent to angle CPT because they are vertical angles.

Therefore, triangle BQP is congruent to triangle CTP by SAS.

Therefore, segment TC is congruent to segment QB by CPCTC.

Well, TC and QB are the radii of circles T and Q respectively. Therefore, circle T is congruent to circle Q.

By similar argument, circle R is congruent to circle T, and Circle S is conguent to circle T. Therefore, by transitivity, all four circle are congruent to one another.

By similar argument, circle S is congruent to circle T, circle R is congruent to circle T and therefore, all four circles are congruent to each other (by transitivity). QED.

RETURN