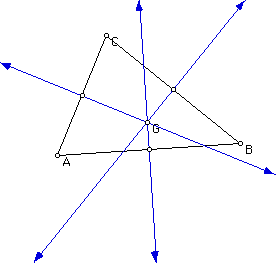
Looking at the sketch below of the circumcenter, G, it is clear that the perpendicular bisectors of the sides of a triangle are concurrent at a single point. For any type triangle, whether obtuse, acute, right, or equilateral, the perpendicular bisectors intersect at one point. When discussing this in a high school geometry classroom, it is not too much to expect the students to be able to prove this theorem. Once they have seen that the perpendicular bisectors are concurrent, the teacher can talk about why this happens.

One proof is as follows:
Looking at the following figure, we know that there is a unique circle containing each of the three points, B, C, and D.
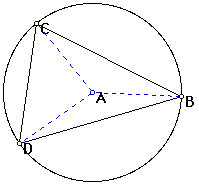
Letting A be the center of this circle, AB is congruent to AC, AC is congruent to AD, and AB is congruent to AD. Since A is equidistant from B and C, then it must lie on the perpendicular bisector of BC. Likewise, A is on the perpendicular bisectors of CD and BD, so that the three perpendicular bisectors are concurrent at A. In addition, we know that the point of concurrence is the center of the circle that circumscribes the triangle, commonly referred to as the circumcenter.