
Assignment 10 Parametric Curves
Write up #2
For various a and b, investigate x = cos(at) and y = sin(at) for t on the fixed interval [0,2Pi].
1. When a =1 and b = 1 we get a circle.

2. When a = -1 and b=-1 we also get a circle. The same thing is true when either a or b is negative and the other is positive. In general, for both a and b greater than or equal to 1, we get a circle when a = b or a = -b.
3. When a and b both are between 0 and 1 or between 0 and -1,
we do not get a full circle. For example, the following graph
is when a = 1/4 and b = 1/4. This is only a fourth of a circle.

In order to get a full circle, we have to increase the interval for t to [0,8Pi]. In general, for an integer n (not zero), for a = 1/n and b = 1/n to make a complete circle, t has to run on the interval [0, 2nPi].
4. Fix a = 1 and vary b. In the first graph, b =2, and the second graph b=3. When b = 2, we get a nice bowtie. We can conclude that varying b gives us different number of leaves arranged on the x-axis as is apparent from the graphs as long as b is an integer different from zero. This means that we have n number of leaves.


5. Fix b=1 and and very a. This is certainly very interesting since we get different patterns of graphs depending on when a is even or odd. In the first four graphs below, a = 3, 5, 7, and 9 respectively. This is very similar to the case above (in number 4) except that the leaves are arranged on the y-axis instead of the x-axis. The last four graphs correspond to
a =2,4,6, and 8. This is quite hard to describe. One observation is that the number of y-intercepts in each case corresponds to |a| . For example, when a = 2, the graph has two y-intercepts and so on.






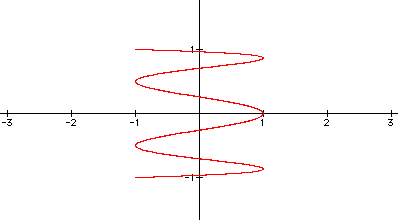

In conclusion, varying a and b has different effects on the graphs as we saw above on the fixed interval of [0,2Pi]. One very common feature to all the graphs above regardless of the values of a and b is the fact that both the domain and range of these graphs is [-1,1].