Assignment 11 Polar Equations
Write up #1
Investigating
![]()
In all the following graphs, the angle is between 0 and 360 degrees.
1. The "basic" graph with a =1, b=1, k=1.
2. Keep b =1, k = 1, and vary a.
When a = -1, there is no difference.
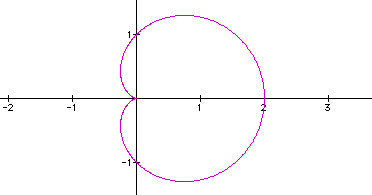
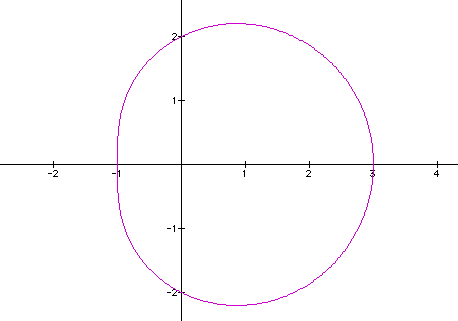
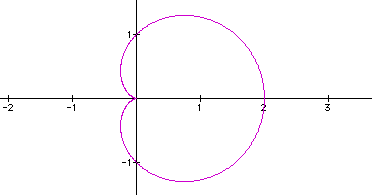
The second graph is when a = 2 or -2. From these two graphs we can conclude that changing the signs for a doesn't make a difference if we keep the other two constant. We can also conclude that as |a| becomes larger, the figure becomes bigger and bigger and resembles a circle more and more.
3. Still vary a, but this time let |a| < 1.
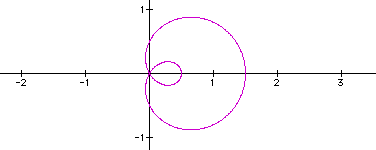
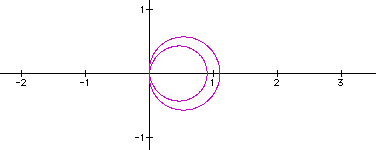
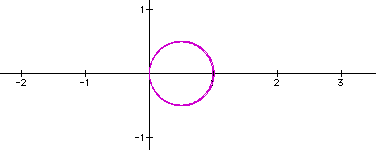
In the previous three graphs, a = 0.5, 0.1, and 0.01 respectively. One can see changes going on at the origin. The point at the origin in the basic graph keeps moving to the right until on the third graph, it becomes a circle that is tangent to the y-axis. In the second graph, we see what looks like two tangent circles. As we keep decreasing |a| there is really no change to the third graph.
4. Keeping the others at 1 but varying b, we get the following graphs.
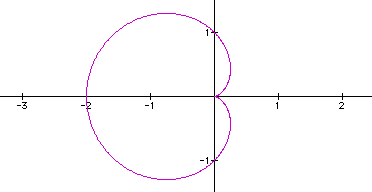
In the previous graphs, a = -1, -2 and 2 respectively. We can see that changing the signs from positive to negative changes the position of the graphs from left to right. In other words, when a = -1, we just get the reflection of the "basic" graph across the y-axis.
5. Still vay b, but this time let |b|<1. As the |b| approaches 0, the graph approaches a circle of radius 1 centered at the origin. In the following graphs, b = 0.5, 0.1, 0.01, 0.001 respectively.
6. Now let's keep a = 1, b=1, and vary k.
In the above four graphs, k is changing. In the first graph, k = -1. In this case, there is really no change to the basic graph. In the second, third, and fourth graphs, k = 2, 3, 4, respectively. Also k = -2, -3, and -4 produce exactly the same results. This is the "n-leaf rose" where n is any interger and a = b. The "roses" are arranged around the origin.
7. Still vay k, but this time let |k|<1.
In the above three graphs, k = 0.5, 0.1 and 0.001 respectively. We can see that as |k| approaches 0, the graphs approach a circle of radius 2 centered at the origin.
8. Comparing with
for various k.
This is very similar to #6 above where we kept the other two at 1 and varied k. There are also some differences. For example, when k = 1, we get different graphs. In this case, it is a circle of radius 0.5 centered at (0.5, 0) making it tangent to the y-axis. This is the same circle in the third graph of #3 above. On the other hand, when we can see that when k = 2, we get four leaves arranged at the origin. But when k = 3, we get only three leaves. This is is similar to #6 above. When k is odd, it is exactly the same as #6. But when k is even, we get twice as many leaves. That is to say that when n is odd, we get n number of "roses" but when n is even we get 2n number of roses.
9. Comparing with
These are very similar graphs to the ones in #1 - 8 above. For example, in the first graph a = 1, b= 1, and k = 1. In the second graph, a =1, b = -1 and k = 1. In the third graph, a = 1, b = 1, and k = 2. In the fourth graph, a = 1, b =1, and k = 3. We can conclude that with appropriate reflections or rotations, we can get the counterparts from #1 - 8 above.