Different values of a, b, and c affect the graph of y in a different way. First of all, a has to be different from 0. Otherwise, we get a linear function instead of quadratic.
1. Here is the graph of 
where a = 1, b=0, and c = 0.
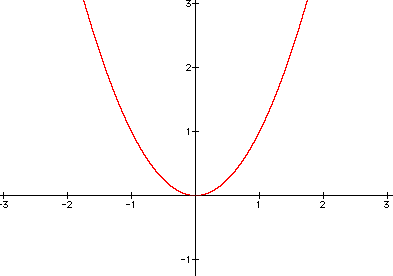
This is the basic graph with a =1, b=0 and c=0. We will talk about changes to this graph as we change the values of a, b, and c.
2. Keeping b = 0, and a
= 1, and varying c, we can see the change in
as follows.
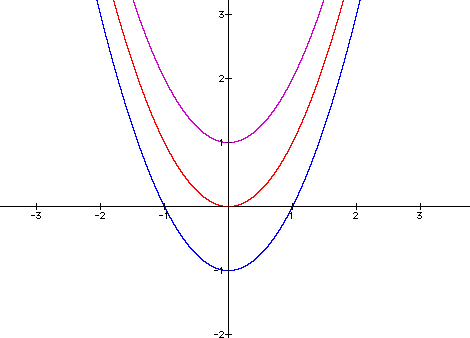
Movement along the y-axis by one unit. When c = 1, the graph moves up by one unit. And when c = -1, the graph moves down by one unit.
3. Keeping c = 0, and a = 1, and varying
b, we can see the change in as
follows.
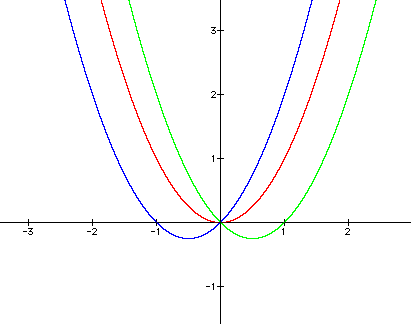
One of the x-intercepts has moved to the right and the other one to the left by one unit. The vertex has also moved down by 1/4.
4. Keeping b = 0 and c
= 0 and varying a, the change in
as follows.
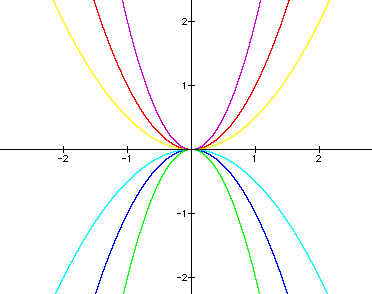
When a = 1/2, the graph is a lot wider than when a = 2. Also when a = -1, the graph is inverted upside down.
5. Similarly we can also look at 
when is a perfect square for different values of h.
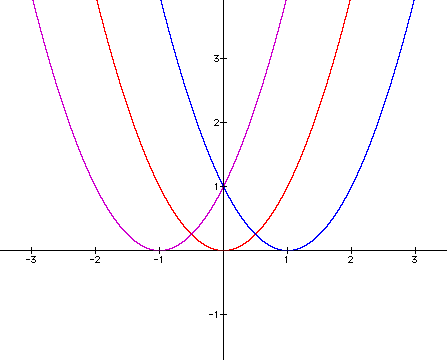
Movement along the x-axis. When h = 1, the graph moves one unit to the left and when h = -1, the graph moves one unit to the right.
Conclusion
The graph of
is affected differently when we use different values of a,
b, and c. For y to be a quadratic function, a
has to be different from 0. Compared to the graph of ,
when a = -1, b = 0 and c 0, the whole graph is inverted upside
down. In other words, the graph is just the mirror image of that
of across the x-axis. Keeping a
= 1 and b = 0, and varying c, we can see that the graph of moves up along the y-axis by c units or
moves down by c units if c is negative. If we keep c = 0, a =
1 and vary b, we can see that the x-intercepts change. It adds
one more x-intercept and also moves the vertex of the graph of
down. Similarly,
varying a and keeping the other two constant will have
an effect in the width of the graph. The graph is a lot wider
when |a| < 1 than at any other time. We can also look at
when is a perfect square for different values of h. It moves the graph of |h| units to the right or to the left on
the x-axis. When h is positive, the graph moves to the left and
when h is negative, the graph moves to the right on the x-axis.