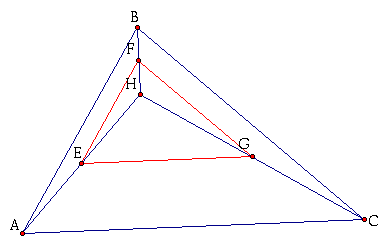
Prove that triangle EFG is similar to triangle ABC.
EG = 1/2 AC, EF = 1/2 AB, FG = 1/2 BC since E, F, and G are midpoints of HA, HB, and HC respectively.
EG/AC = EF/AB = FG/BC = 1/2.
Therefore, triangle EFG is similar to triangle ABC since the ratios of the corresponing sides are equal (1/2).
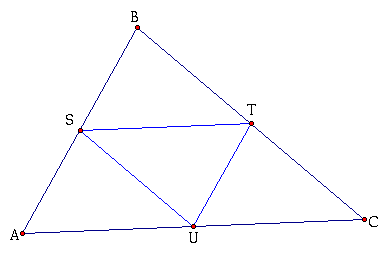
Prove that triangle EFG is congruent to triangle TUS, which is the medial triangle of the same acute triangle ABC.
EG = 1/2 AC, and so is ST. -> EG = ST
EF = 1/2 AB, and so is UT. -> EF = UT
FG = 1/2 BC, and so is SU. ->FG = SU
Therefore, triangle EFG is congruent to triangle TUS as required.