Assignment 8 Altitudes and Orthocenters.
Write up #12
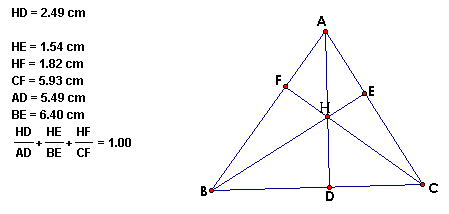
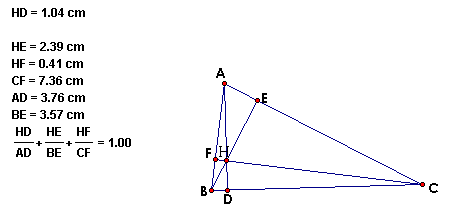
Given triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectively.


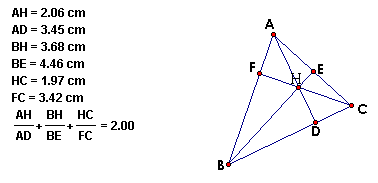
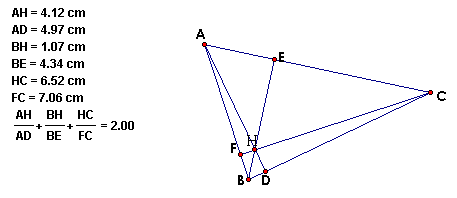
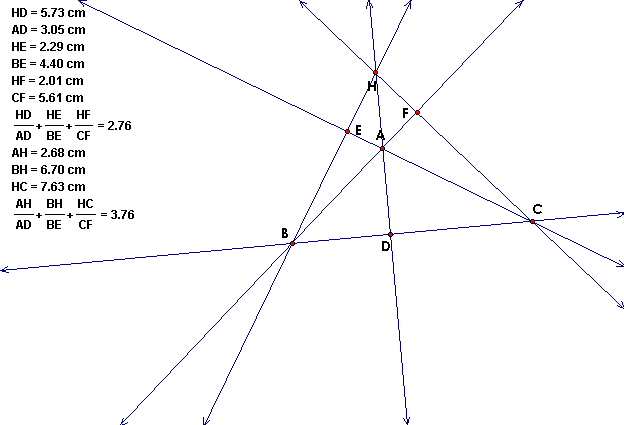
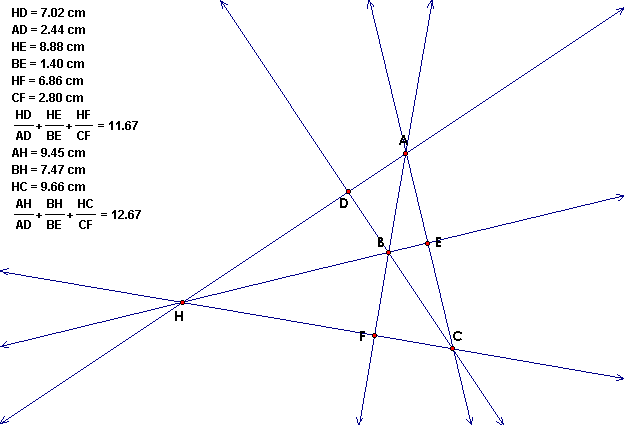
The above sketches in GSP show the sum of the ratios as required when H is inside the triangle.
We can also show this relationship using a specific example of triangle. Let's assume that the triangle under consideration is an equilateral triangle.
HD/AD + HE/BE + HF/CF = 1
Assume that triangle ABC is equilateral. Then the altitudes are also the medians. And medians meet at a point that is two-thirds of the way from the vertex to the opposite side. This means that HD/AD = HE/BE = HF/CF = 1/3. Therefore 1/3 + 1/3 +1/3 = 3/3 = 1 as required.
AH/AD + BH/BE + CH/CF = 2
Using the same reasoning as above, AH/AD = BH/BE = CH/CF = 2/3 and 2/3 +2/3 +2/3 = 6/3 =2 as required.
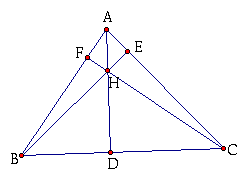
However, this relationship will not hold when triangle ABC is an obtuse triangle. In other words, the above relationship is not true when H is outside of triangle ABC. The two figures below illustrate this. The triangle is made of lines instead of segments to show the relationship for an obtuse triangle.