Assignment 9 Pedal Trangles
1. Pedal triangle when P is any arbitrary point on the plane of the orginal triangle.

Here P can be anyhwere in the plane of triangle ABC and we don't always get a pedal triangle. When one of the vertices of the pedal triangle coincides with one of the vertices of triangle ABC, we do not have a pedal triangle. We also do not have a pedal triangle when P lies on one of the vertices of the triangle ABC.
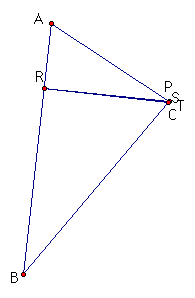
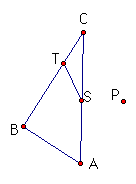
In the first case above, P is at vertex C of triangle ABC and it seems like all the four points P, S, T,and C have converged to one point thus preventing the formation of the pedal triangle. In the second case, point R is at vertex A and again, we don't have a pedal triangle.
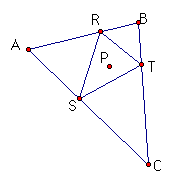
2. Pedal triangle when P is the centroid of the original triangle.
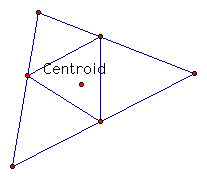
Since the centroid is always inside the triangle, we will have a pedal triangle as long as one of the vertices of the pedal triangle is not on one of the vertices of the orginal triangle, as is the case in the second picture above.
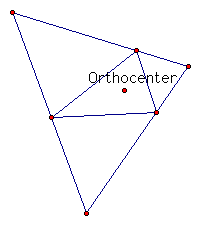
3. Pedal triangle when P is the orthocenter. Since the orthocenter is not always inside the triangle, we get a pedal triangle only when the orthocenter is inside the triangle. When the orthocenter is on one of the vertices as in the case of the right rtiangle below in the second picture, we do not have a pedal triangle. The same thing is true when the orthocenter is outside the triangle as in the case of the third picture. Also when the orthocenter is outside the triangle, one of the vertices of the pedal triangle, one of the vertices of the orginal triangle and the orthocenter lie on the same line. This is apparent from the third picture below.