Final Assignment
Part Two
A. Consider any triangle ABC. Select a point P inside
the triangle and draw lines AP, BP, and CP extended to their
intersections with the opposite sides in points D, E, and F respectively.
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and
various locations of P.
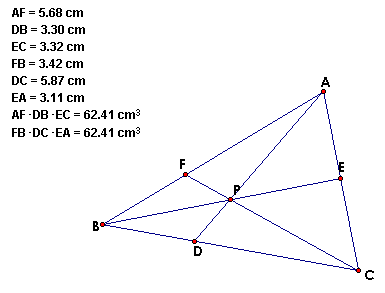
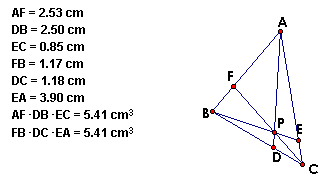
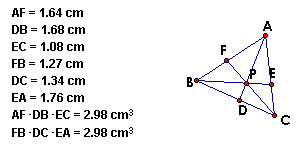
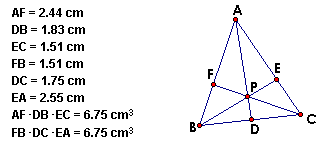
From the above four triangles, we can see that (AF)(BD)(EC)
= (FB)(DC)(EA).
B. Prove the above.
We can get the following figure by constructing lines through
B and C parallel to AD and extending their intersections through
CF and BE. The three segments BX, AD, and CY are parallel.
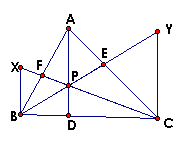
Because of equal vertical angles and equal interior angles,
triangle AFP ~ BFX, and triangle CEY ~ AEP. From
this similarity, we can get the following ratios:
AF/BF = AP/BX and CE/AE = CY/AP
Because of the common angles and equal corresponding angles,
triangle BDP ~ BCY and triangle BCX ~ DCP . And the following
ratios:
BD/BC = DP/CY and BC/DC = BX/DP.
Now let's multiply the left and the right sides of these equations
to get
(AF/BF)(BD/BC)(BC/DC)(CE/AE)=(AP/BX)(DP/CY)(BX/DP)(CY/AP) and
simplifying we get,
(AF/BF)(BD/DC)(CE/AE) = 1 and this means that (AF)(BD)(CE)
= (BF)(DC)(AE) as required.
And this ratio will also hold true even when the point P is
outside of triangle ABC as shown below.
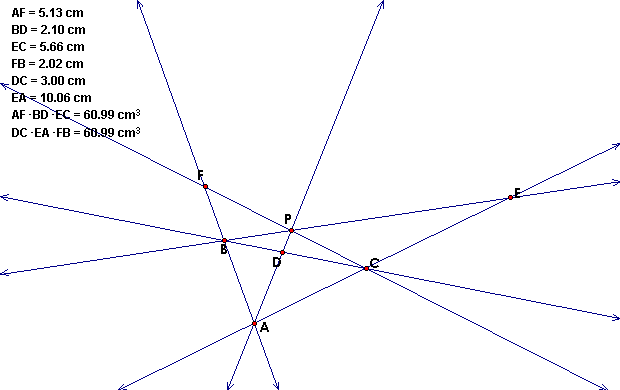
GSP Sketch
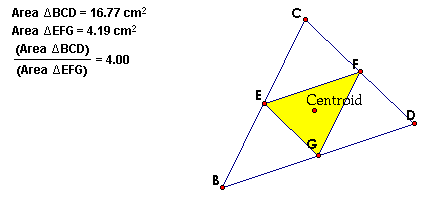
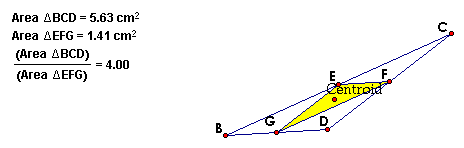
C. Show that when P is inside triangle ABC,
the ratio of the areas of triangle ABC and triangle DEF is always
greater than or equal to 4. When is it equal to 4?
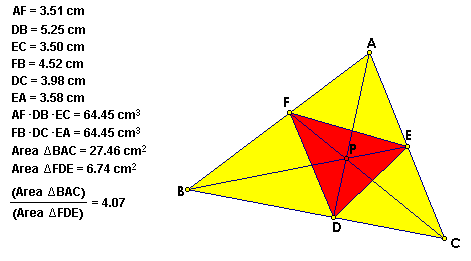
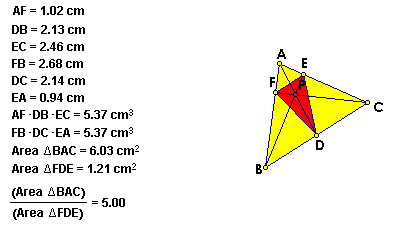
GSP Sketch
The above two figures show that the ratios are greater than
or equal to 4.
The ratio is exactly 4 when P is the centroid of the triangle
as shown below.
GSP Sketch
Part Three
Course Evaluation sent to PWILSON@coe.uga.edu.
RETURN









