Different values of a, b, and c affect the graphs of
y = a sin(bx + c) in a different way.
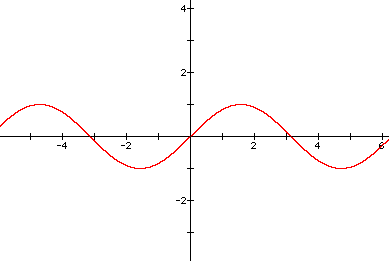
1. Graph of y = sinx
This is the basic sine graph and we will compare the effects of a, b, and c on y = sinx to this basic graph.
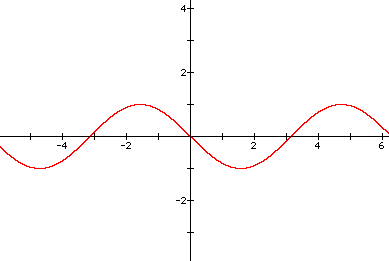
2. Graph of y = -sinx
This is just the reflection of y = sinx across the x-axis.
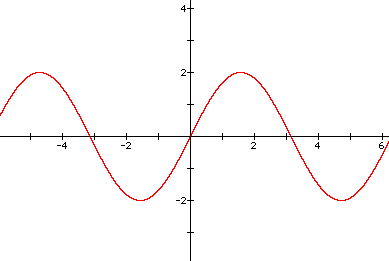
3. Graph of y = 2sinx
The range of the y = sinx is [-1,1]. But the range of this function is [-2,2]. In other words, the amplitude of this function is twice that of y=sinx.
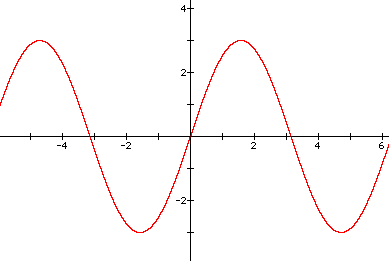
4. Graph of y = 3sinx
The range of the y = sinx is [-1,1]. But the range of this function is [-3,3]. In other words, the amplitude of this function is three times that of y=sinx.
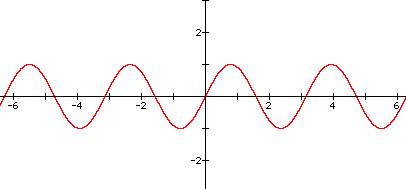
5. Graph of y = sin2x
The period of this function is half that of the function y=sinx. This means that every point on the graph of y = sin2x repeats itself twice within the same interval as that of y = sinx.
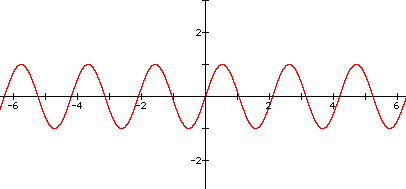
6. Graph of y = sin(3x)
The period of this function is a third of that of the function y=sinx. This means that every point on the graph of y = sin3x repeats itself three times within the same interval as that of y = sinx.
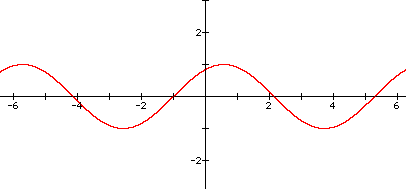
7. Graph of y = sin(x+1)
In this graph, there is a phase shift to the left by one point of every point on the graph of y=sinx.
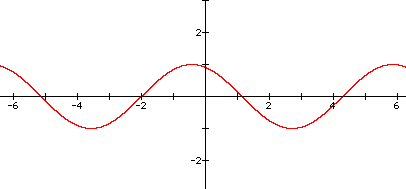
8. Graph of y = sin(x-1)
In this graph, there is a phase shift to the right by one point of every point on the graph of y=sinx.
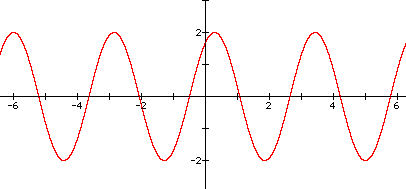
9. Graph of y = 2sin(2x+1)
This graph shows the effects of all the three variables on the graph of y = sinx interacting at the same time.
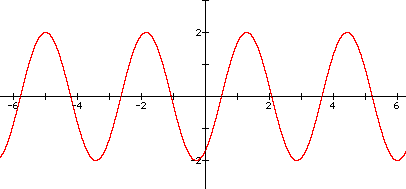
10. Graph of y = 2sin(2x-1)
This graph shows the effects of all the three variables on the graph of y = sinx interacting at the same time. The only difference between this graph and the graph in number 9 above is the phase shift to the right. In number 9, the phase shift is to the left.
Conclusion
Assume that a, b, and c are positive
real numbers. The graph of y = sinx is affected by these variables
differently. In y = asinx, the range of the the function
is [-a,a] and the amplitute is just a. In y = -asinx,
the graph of y = sinx is reflected in the x-axis. For y = sin(bx),
the period is just 
/b. Finally,
for y = asin(bx + c), the phase shift is
by -c/(
).