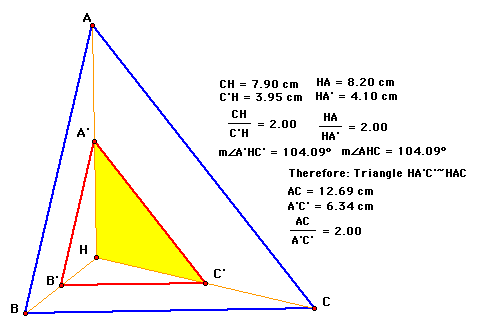
Triangle ABC
A' midpoint of HA
B' midpoint of HB
C' midpoint of HC
Given:
Triangle ABC
A' midpoint of HA
B' midpoint of HB
C' midpoint of HC
Prove triangle A'B'C' ~ triangle ABC
Proof:
By the definition of midpoint, HA'= A'A and HC'=C'C. Then HA = 2*HA' and AC = 2*HC'. Since the angle A'HC' and AHC are the same angle triangles HA'C' and HAC are similar by SAS Similarity Theorem. By the same method, this can be proven that triangles HB'C'~HBC and triangles HB'A'~HBA. From the first similarity relationship the ratio of A'C to AC is 1 to 2. This is also the case for the ratio of B'C' to BC and A'B' to AB. By the SSS similarity relationship, then you can conclude that triangle A'B'C'~ABC. Refer to the following figure for a visual and analytical demonstration of the proof.
Given: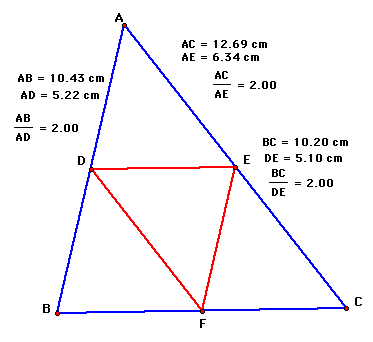
Triangle ABC
D midpoint of AB
E midpoint of AC
F midpoint of BC
Triangle ABC ~ Triangle FDE
Proof:
With a similar procedure as the previous proof, we can use the definition of midpoint to create a relationship between sides AD, AB and AE, AC. By the definition of the midpoint, AD = 1/2 (AB) and AE = 1/2 (AC). Then the ratio of the two pairs of sides (AD/AB) and (AE/AC) are both 1 to 2 (1/2). Also since angle A is congruent to itself, we again have a SAS similarity relationship. Thus, triangle ADE ~ triangle ABC. By the same approach we can show that triangle CEF ~ triangle CAB and triangle BDF ~ triangle BAC. From these similar triangles the sides of the medial triangle (DE, EF, and FD) correspond to the larger triangle as well. (BC/DE) = (AB/EF) = (AC/DF) = (2/1). Therefore, triangle DEF ~ to triangle BCA.
Conclusion: By transitivity,
since both triangles A'B'C', and DEF are similar to triangle ABC,
implying that their corresponding angles are all congruent, and
since the ratio of the sides are all 1 to 2 from triangles A'B'C',
and DEF. It is enough to show that triangle DEF is congruent to
triangle B'C'A'.
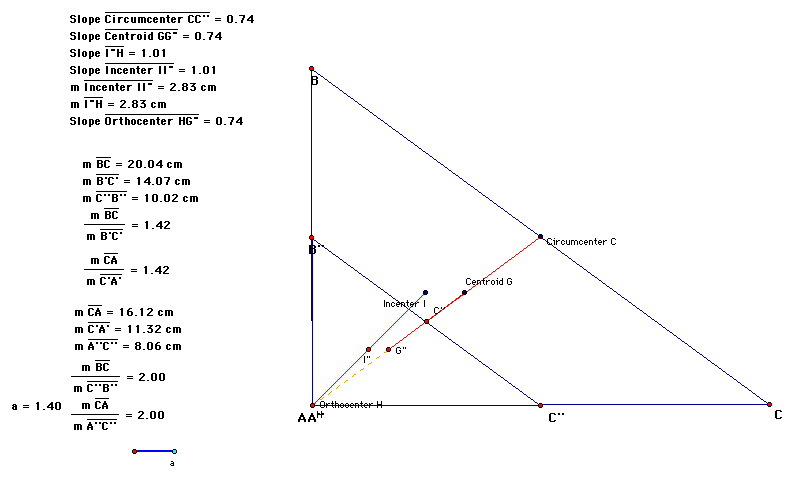
After constructing triangle A'B'C' in the interior of triangle ABC, the incenter (I), circumcenter (C), centroid (G), and orthocenter (H), were constructed in both triangles.
1) Since triangle A'B'C' was constructed from the midpoints
of the altitudes of triangle ABC, both triangles shared the same
orthocenter.
2) The question only asked to take into consideration the situation
for an acute triangle, upon observing
the behavior of the I,C, G, and H the obtuse, and right triangle
case the following could be said:
(GSP examples are given for each different case, click either
obtuse, right, or acute to go to the link)
a. Due to the similarity of the triangles, the proportion of the
segments composing of the orthocenter and incenter of each respective
triangle will be in the same ratio as the ratio of sides for each
triangle.
b. Due to the similarity of the triangles, the proportion of the
segments composing of the orthocenter and centroid of each respective
triangle will be in the same ratio as the ratio of sides for each
triangle.
c. Due to the similarity of the triangles, the proportion of the
segments composing of the orthocenter and circumcenter of each
respective triangle will be in the same ratio as the ratio of
sides for each triangle.
d. In an obtuse triangle condition, triangle
A'B'C' will be found exterior to triangle ABC.
e. In the right triangle condition, triangle
A'B'C' there is one case where the orthocenter of the triangles
will be at the right angle.
f. In the acute triangle condition, triangle
A'B'C' will be found in the interior of triangle ABC.
3) Upon constructing additional similar triangles much of the
properties will remain the same (i.e. similar ratio of sides and
the segments of AB/A'B', HI/HI', HG/HG', and HC/HC'). Click
here ->For a GSP interpretation.
 Acute
Triangle Case:
Acute
Triangle Case:
Right triangle Case:
Questions? E-mail: gt0353d@arches.uga.edu