Assignment 8

Altitudes and Orthocenters

Given:               

Prove:        

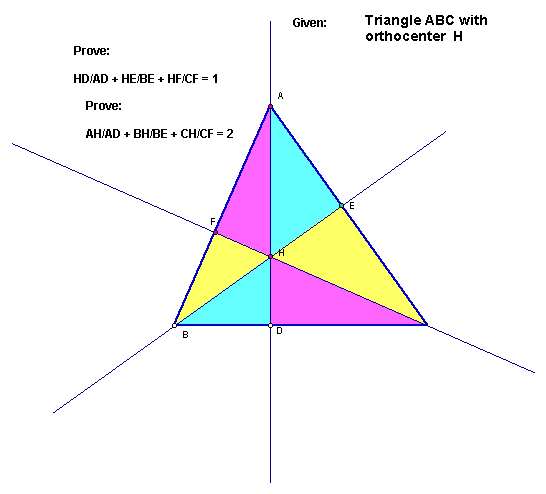
Proof     I:    We can use the area of the triangles formed by the altitudes in addition to the original triangle to show that the sum of the ratio of the sides, HD, AD, HF, CF, HE, and BE are equal to one. First we must establish the area of the triangles:

DHBC = (1/2)(HD)(BC)  DHAB = (1/2)(HF)(AB)   DCHA = (1/2)(HE)(CA)     

DABC = (1/2)(AD)(BC) DCAB = (1/2)(CF)(AB) DCBA = (1/2)(BE)(CA)   

                  The sum of the three triangles HBC, HAB, and CHA, will be equal to the area of the large triangle ABC. So, when we set this ratio up, we take want we want to prove and multiply the corresponding base and 1/2 to get the area of the triangles:

                               (HD/AD)(0.5*BC/0.5*BC) + (HF/CF)(0.5*AB/0.5*AB) + (HE/BE)(0.5*CA/0.5*CA)

this can be re-written as:

(DHBC/ DABC) + (DHAB/ DABC) + (DCHA/ DABC)

(DHBC + DHAB + DCHA) / DABC)

since,

(DHBC + DHAB + DCHA) = DABC

then, by substitution:

(DHBC + DHAB + DCHA) / DABC) = (DABC / DABC) = 1

and,

(0.5*BC/0.5*BC) = (0.5*AB/0.5*AB) = (0.5*CA/0.5*CA) = 1,  we have:

 (HD/AD)*1 + (HF/CF)*1 + (HE/BE)*1 =  (DABC / DABC) = 1

Therefore:

 (HD/AD) + (HF/CF) + (HE/BE) = 1

Given:               

Prove:             equation II.1

 

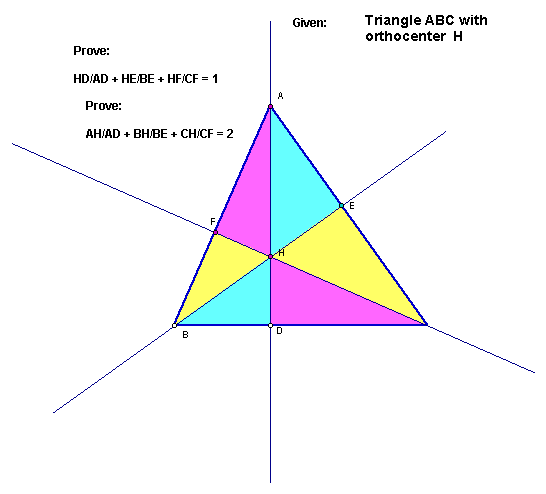
Proof     II:    We can use the properties of the segments to come up with these equations:

AD = AH +DH            CF = CH +HF            BE = BH +HE

By rearranging the equations:

AH = AD - DH             CH = CF - HF            BH = BE - HE

then by substituting it into equation II.1:

[(AD - DH)/AD] + [(CF - HF)/CF] + [(BE - HE)/BE] 

Simplify

[1 - (DH/AD)] + [1 - (HF/CF)] + [1 - (HE/BE)]

3 - [(DH/AD) + (HF/CF) + (HE/BE)]

from previous proof we get:

3 - [1] = 2

Therefore: 

[(AH)/AD] + [(CH)/CF] + [(BH)/BE] =  2

 

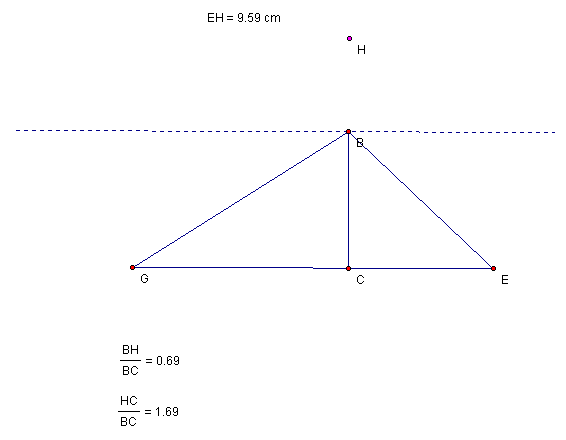
Obtuse Case:    When the triangle is obtuse we get an interesting scenario, where the orthocenter lies in the exterior of the triangle. This will also eliminate segments,  HD, GD, HF, and EF,  leaving segments, EH, and HG. From the GSP sketch you will notice that the analytical results and a very useful phenomena that occurs. When the vertex is moved on a line parallel to the base, the locus of points forms a parabola with a focus at the vertex. Click here for a GSP animation: If you do not have java sketchpad click here for GSP Animation File->

 

                       

Return to Assignment Matrix click here ->

Questions? E-mail: gt0353d@arches.uga.edu