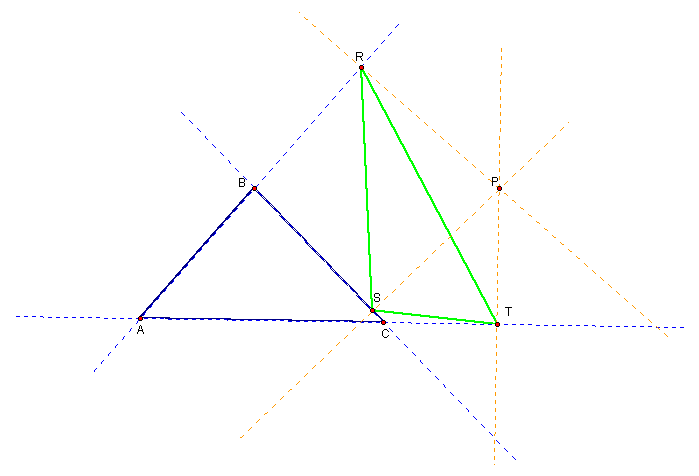
For this following exploration, we need to first construct the pedal triangle for a pedal point and observe the behavior of the midpoints of that triangle. To construct the pedal triangle, following these steps:
1) Draw a triangle ABC (extend the three segments into lines)
2) Place a pedal point, P outside the triangle
3) Construct perpendiculars to each of the three lines: AB, BC, AC
4) Let the intersections be points: R,S, and T
5) You now have triangle RST as the pedal triangle.

For the GSP sketch and script tool click here ->
Now, for the exploration, a circle is drawn where the radius is greater than the radius of the circumscribed circle of triangle ABC. The midpoints of the pedal triangle are constructed.
Before we jump into any exlporation, it would be helpful to think about the types of relationships we are looking for. We can also divide our exploration into three parts with respect to an acute, obtuse, or right parent triangle ABC.
What would the locus of points look like for each case, obtuse, acute, and right? What kind of relationships can we develop with our knowledge of pedal points, pedal triangles, etc....
Now, we are ready to explore the GSP sketches.
To explore each case click below:
After viewing each different case, the following observations could made and further explored:
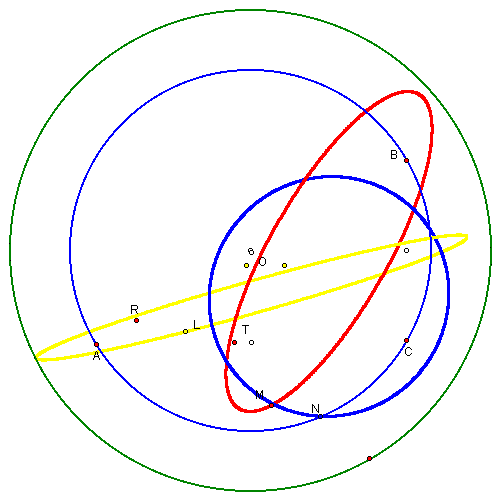
For the Right triangle case, the path of the midpoints of the pedal triangle seem to construct two ellipses and a circle. For the obtuse triangle case, locus of points seem to construct three ellipses. Similarily, for the acute triangle case, the locus of points seem to construct three ellipses as well. But, for the acute case, the ellipses are "thinner" than the obtuse case. This would provoke the observer to correlate some kind of relationship between the angle measure and eccentricity of the locus of points.
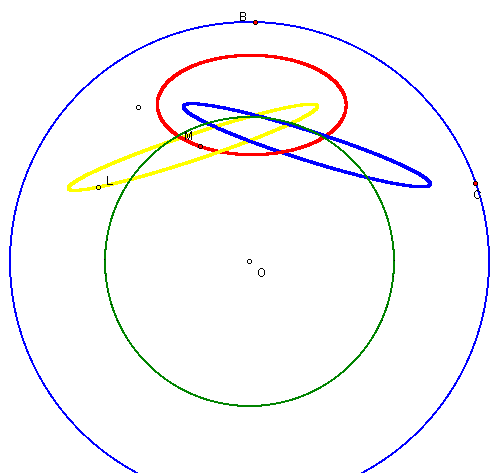
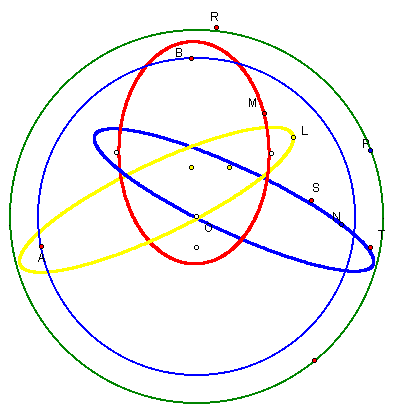
Note that the red, blue, and yellow ellipses are the locuse of points for the midpoint of the pedal triangle.
Return to Assignment Matrix click here ->
Questions? E-mail: gt0353d@arches.uga.edu