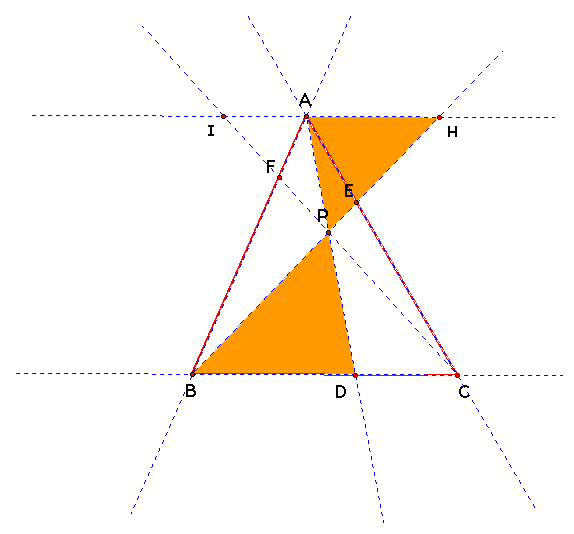The Last One!
Final Project
II.a)
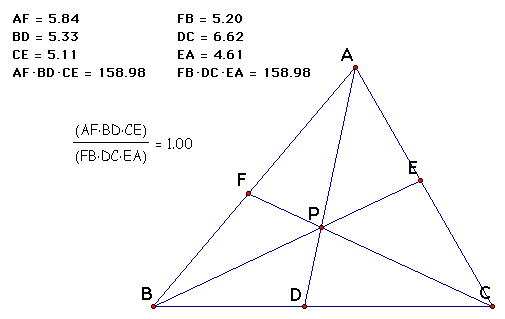
For different locations of P, The ratio of (AF*BD*CE ) / (FB*DC*EA)
will always be one. To observe an example please click
here ->
II.b)
Proof:
Given:
Triangle ABC with Point P interior to ABC
Prove:
(AF*BD*CE) / (FB*DC*EA) = 1
Let Line L be parallen to line
BC. By vertical angles, alternating
interior angles we have similarity between the following triangles:
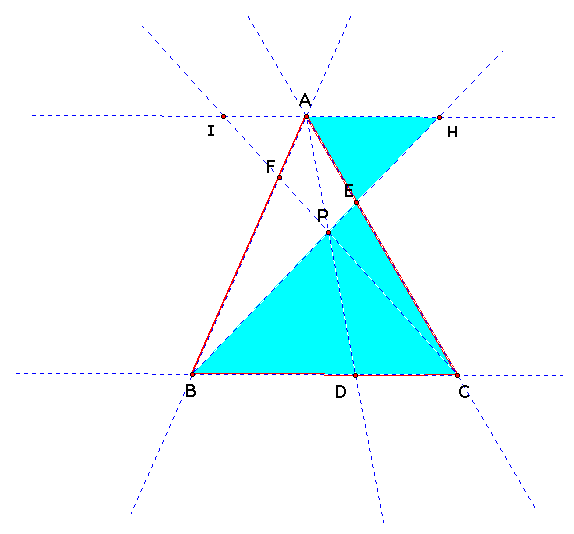Triangle AEH ~ Triangle
CEB
Where the following Properties Hold:
AE/CE = EH/EB = AH/CB
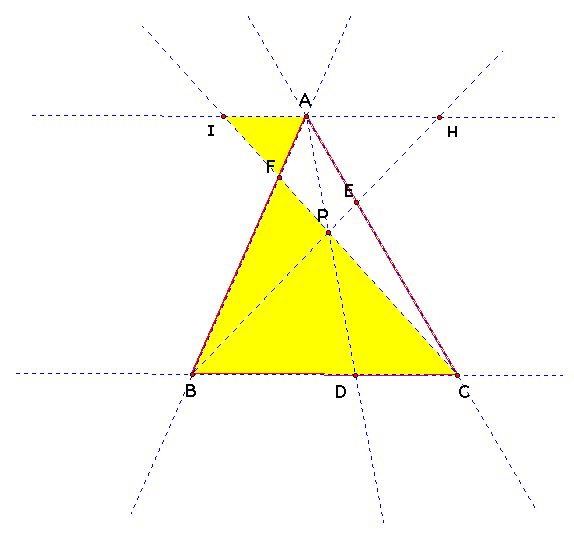
Triangle AFI ~ Triangle BFC
Where the following Properties Hold:
AF/FB = FI/FC = AI/BC
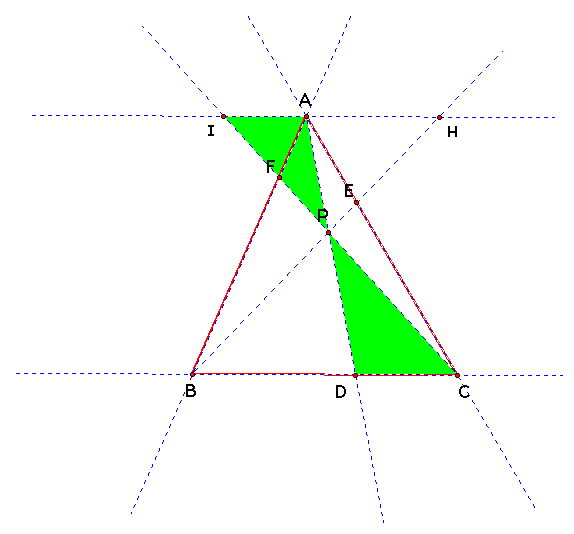Triangle AIP ~ Triangle
DCP
Where the following Properties Hold:
AI/DC = IP/PC = AP/PD
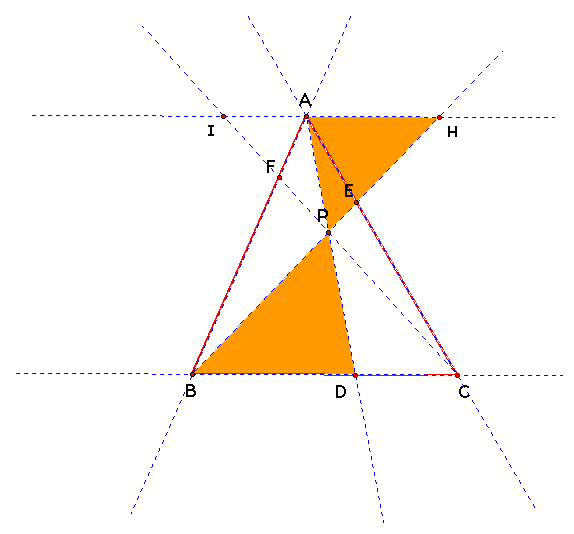
Triangle APH ~ Triangle DPB
Where the following Properties Hold:
AH/BD = PH/PB = AP/PD
We have the following similarity relationships:
AH/BD = PH/PB = AP/PD (Eq.1)
AI/DC = IP/PC = AP/PD (Eq.2)
AF/FB = FI/FC = AI/BC (Eq.3)
AE/CE = EH/EB = AH/CB (Eq.4)
From Eq.4 we get:
AH = (BC*AE)/EC (Eq.5)
From Eq.3 we get:
AI = (BC*AF)/FB (Eq.6)
From Eq.1 and Eq.2 we get:
(AI/DC) = (AH/BD) (Eq.7)
By substituting Eq.5 and Eq6. into
Eq.7 =>
[(BC*AF)/(FB*DC)] = [(BC*AE)/(EC*BD)]
Cross multiply:
[(BC*AF)*(EC*BD)] = [(BC*AE)*(FB*DC)]
solve for BC
BC*[AF*EC*BD] = BC*[AE*FB*DC]
BC/BC = [AE*FB*DC]/[AF*EC*BD]
1 = [AE*FB*DC]/[AF*EC*BD]
II.c)
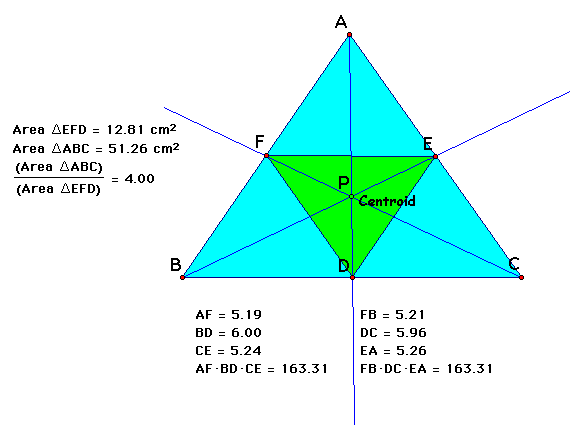
The ratio of triangle ABC to triangle
EFD will equal four only when P is at the centroid of triangle
ABC. The ratio will always be four, if you don't believe me, attempt
to find a ratio below four for by moving P anywhere in the interior
after you click here -> (w javascript)
(w/o javascript)
Return to Assignment
Matrix:
Questions? E-mail: gt0353d@arches.uga.edu