

In this assignment, We are constructing various graphs for the parabola represented by:
for different values of a,b and c. (a,b and c are elements of the rational numbers). Some explanation will be provided initially with more detail regarding the graphs to follow.
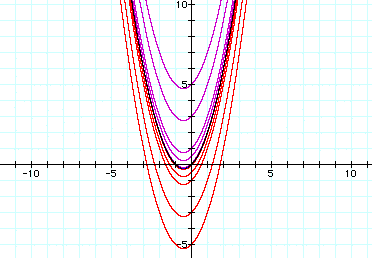
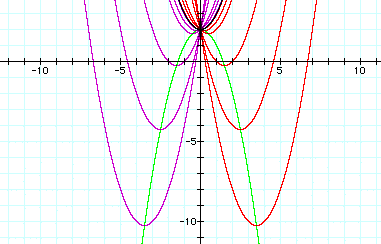
In the previous picture, c = values ranging from -5, -.05, -.5, 0, .05 ... to +5. Admittedly, there is overkill. If you notice the area in the middle where the color appears black, there are 3 parabolas. (The dark colored parabola is sandwiched between a red and purple parabola). The middle parabola is y = x^2 +x, (c = 0). All of the rest of the parabolas vary above or below this 'parent' parabola. The parabolas that rest above the parent have c values > 0, while the ones resting below have c values < 0. The smaller the positive/negative c value, the closer that particular parabola is to x^2 + x. As c gets smaller and smaller either from the positive or negative direction, the function approaches x^2 + x.
The next picture will show 9 different values of a. The variables b and c are fixed; b = 1 and c = 2.
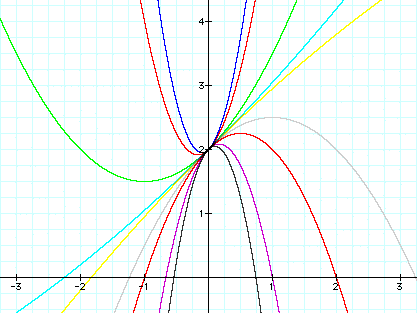
Notice that all the graphs cross in the same place. They all intersect at the same point, (0,2).Obviously, the "+ 2" in the equation accounts for this. Note that the two lines, light blue and yellow, are almost straight when intersecting the point (0,2). These two lines are almost the same as the function y = x+ 2. The x + 2 function would be a straight line with slope of +1 through the point (0,2). If you above the 2 central lines, you'll see that the green, red and blue parabola's are concave up (positive) above the ~ x +2 function and the rest are concave down below the ~ x + 2 function.
So far the variables a and c have been examined; now we will vary b while a =1, c =2.
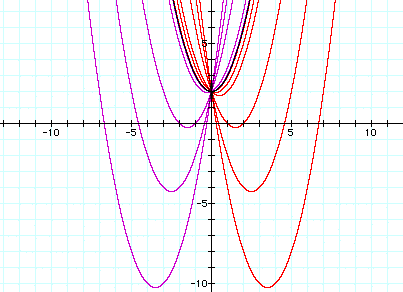
It is apparent that the set of purple parabolas move down to the left from the 'highest' parabola of x^2 + 0x + 2. As the coefficient of x becomes greater positively, the parabola dips lower and lower to the left. As the coefficient of x becomes greater negatively, it dips lower to the right. All of the parabolas have an upper limit; they cannot climb higher than the x^2 + 2 parabola. (Note, what parabola is missing in this picture?)
More in-depth investigations:
To start, the ranges on the graphs will be adjusted for purposes of interpretation; The series of graphs will be analyzed in the same order as was done previously.
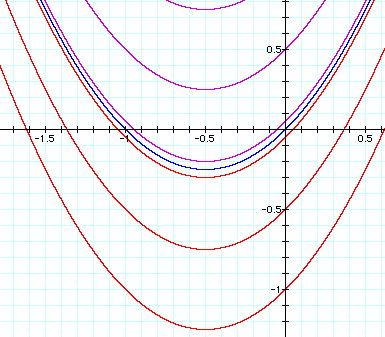
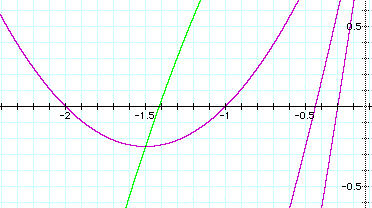
Notice that the minimum (lowest) point is centered at the -0.5 value. One could draw a vertical line through all the graphs just to connect them just to show that all the graphs have minimums centered here. The question is : Why do all the graphs have minimums at this particular point?
The following graph might shed light on this:
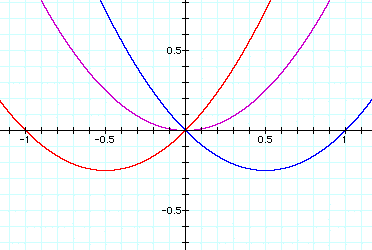
The red parabola is x^2 + x, the blue is x^2 - x, while the purple is x^2. (Due to the range, x^2 + 2 would have been out of view, hence the reason for just x^2; it still gives the desired effect). The factor, + x with x > 0, is what shifts all the parabolas to the left of the y - axis. Observe that the - x factor w/ x > 0, shifts the parabola to the right of the y axis. Obviously, the red and blue parabolas are symmetric to the y axis (resulting in being the same distance apart from each other) as well as the x^2 parabola. FYI: Due to symmetry, if one were to connect the minimum points and the origin to each other the result would be an isosceles triangle.
The graphs with -a- varied are examined next:
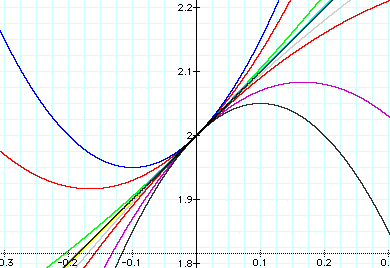
Note, the graph y = x + 2 has been added. It is the black line in the center. This has been added for reference. Since c = 2, all the graphs connect at (0,2). If one visualizes these graphs, as you move starting from positive values on the y axis down through the origin through negative values of the y axis, the graphs open, become straight (at y = x+2), and begin to close. This 'pivot point' is where they connect (0,2). Whatever the coordinates are for c, they determine the pivot point for all the graphs in this picture.
The graphs with b varied are examined next:
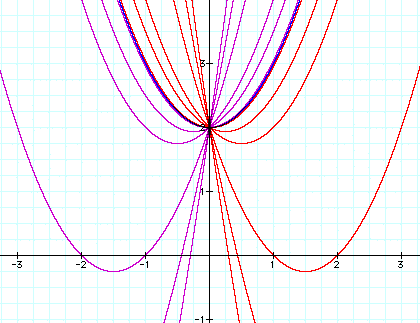
The symmetry is interesting. It becomes apparent that the minimum values for the parabolas in red fit the expression of -b/2. This is most apparent for the red graph of x^2 -3x +2; the minimum value is at +1.5 -> the negative of 1/2 of -3 (-1/2*b). For x^2 +3x +2 ,in purple, note that -b/2 = -1.5. The same holds true for all. See the next picture if unsure:
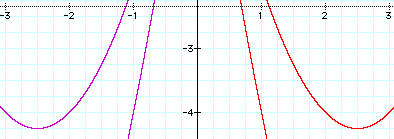
The purple graph is x^2 + 5x +2 and the red = x^2 -5x +2. Finally, note that there seems to be a parabola that fits within all of the other parabola's whose 'arms' pass through all the minimum values and whose maximum is at (0,2). The function is y = -x^2 +2.
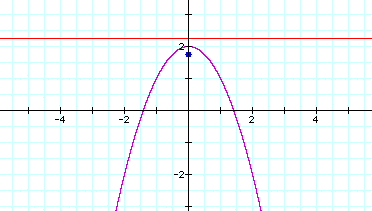
The focus for this parabola is (0,1.75) with directrix y= 2.25:
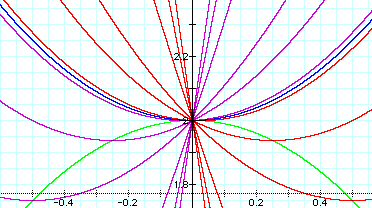
Click HERE to see the movement of ax^2 + bx + c with respect to time. Try to identify which moving graph corresponds to the three variations of ax^2 + bx + c that was discussed. To start the movie, click on the lower left arrow; To close, click on the upper left box.
I believe for demonstration, if 5 graphs were produced then careful explanation is required to avoid any confusion. If 1 graph at a time were demonstrated, one would need an explanation for each one and then a summary of all the graphs to avoid confusion. In all cases, an explanation is essential.