

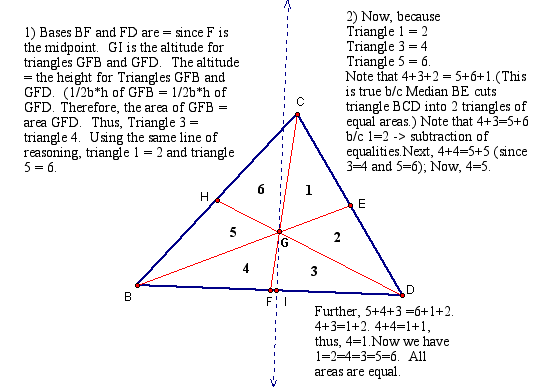
1. The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. Every triangle has three medians; the point at which the medians cross is always located inside the triangle. If three or more coplanar lines intersect at the same point, they are concurrent lines. The point of intersection is the point of concurrency. The point of concurrency of the medians of any triangle is the centroid. The centroid is the center of balance or gravity of the triangle.
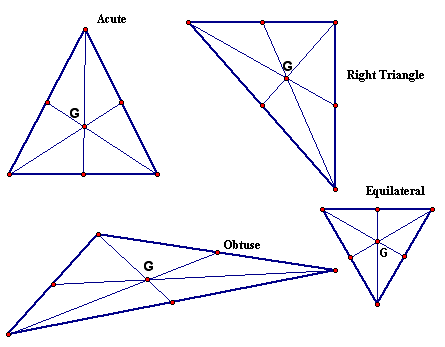
An interesting fact to note is that the centroid divides each of the medians into the same ratio. In the following picture the medians of the acute and obtuse triangles were measured and the ratios are compared:
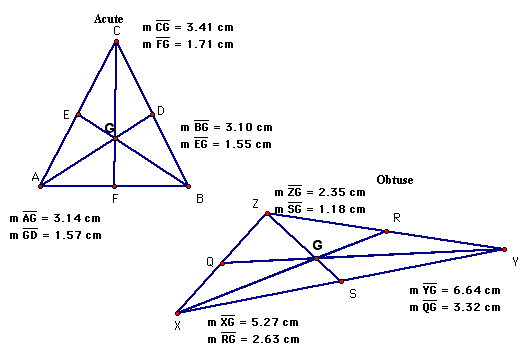
It is interesting to observe that, for each median, the longer segment is two times longer than the shorter segment. That is, there is a ratio of 2:1 of the longer:shorter segments. This fact holds for the right and equilateral triangles as well.
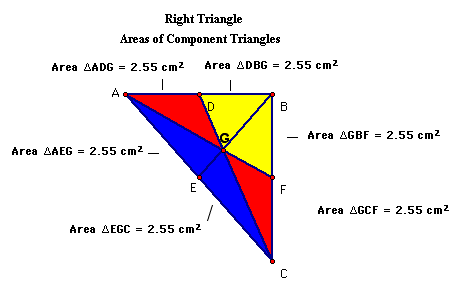
When the areas of the six triangles created by median construction of a right triangle are compared, one finds that they are all equal in value (not in shape):
The same is true for just two triangles formed by only one median construction. In the left triangle, the two triangles are formed from the median AE. In the right triangle, the median MR divides triangle MNO into the red and blue triangles.
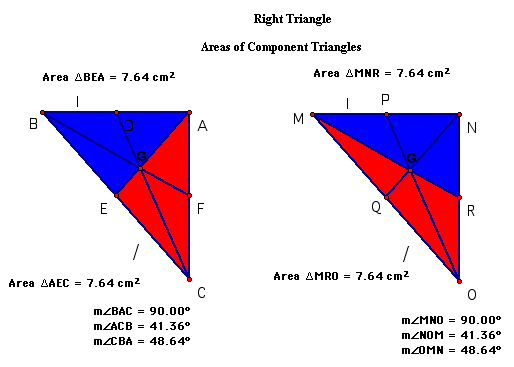
This fact holds for the acute, obtuse and acute triangles as well.
The following is a proof for equal areas for the six triangles:
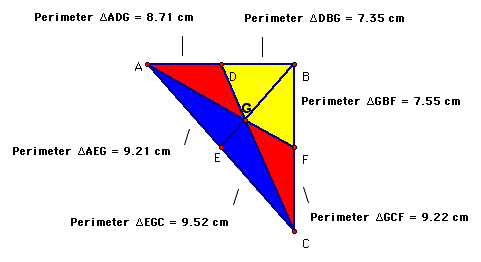
When the perimeters are compared, it is immediately evident that none of the individual perimeters are equal to any other:
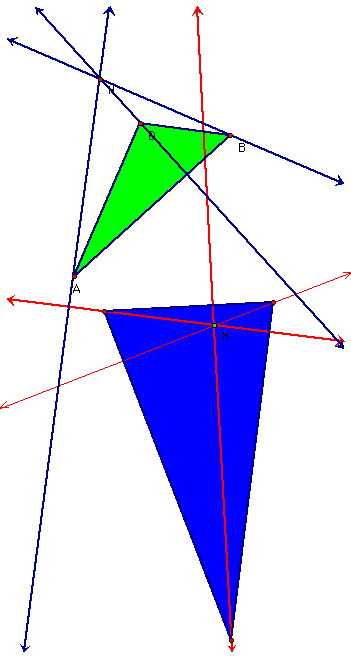
An ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. Note that point H does not have to be on the segments that are the altitudes. Rather, H lies on the lines extended along the altitudes (H can lie outside the triangle).
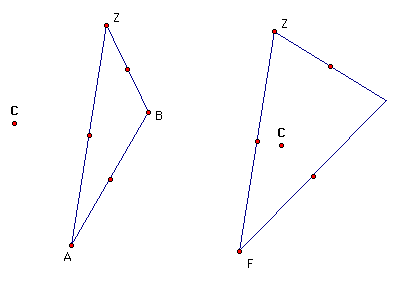
The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. It is possible that C may be outside of the triangle.
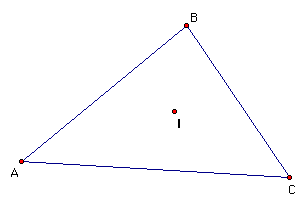
The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then (I) must be on the angle bisector of each angle of the triangle. The incenter remains inside the triangle:
Constructing a smaller triangle by connecting the three midpoints of the larger triangles' sides is called a Medial triangle. It is similar to the original triangle and is one-fourth of its area. The medial triangle is in the red. For clarity, points for the red triangle are labelled with a prime (').
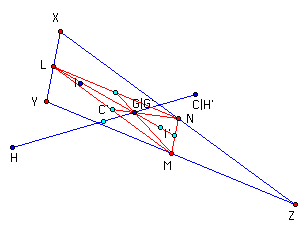
Note that all four small triangles have one-fourth of the area of the larger triangle. Point C|H' refers to both triangles. C is the circumcenter of the blue triangle while, H' is the orthocenter of the red. They exchanged places. The circumcenter for the red triangle is point C'. This point is located below the label C' and is found on the blue segment connecting C|H' - G|G' - C' to H. Both G and G' represent the same point - that being the centroid of both triangles. Note that H is the orthocenter of the blue triangle. In this picture, the incenters for both are non-colinear with the other points. It's interesting to note that when massaging the picture, point H exits the triangle only through the vertex of its respective triangle. Point C exits its respective triangle only through the midpoint of the sides.