

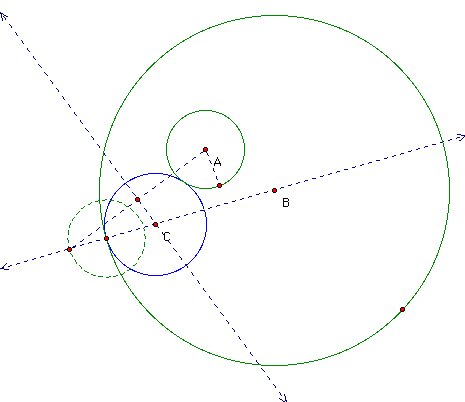
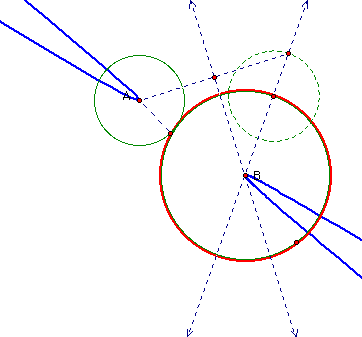
Tangent circles, their constructions and the loci of their centers provide an interesting and informative investigation. The following picture shows a typical construction of a tangent circle. A random circle was constructed (B) followed by circle A. A random point was placed on B (in this case). Here, the radius of A was added to the random point and the dashed circle was constructed. A segment was made from the center of A to the farthest point on the dashed circle. A perpendicular line was formed at the midpoint and the intersection of that line and the diameter through B defines the center of the tangent circle in blue. Circle C was constructed by center and the random point. Thus, the Tangent Circle is born. Variations in the construction include placing the random point on the small circle, adding the radius of the other circle (B, here) to A; creating a perpendicular bisector on a segment from the center of say, A, as in this construction, to the point of intersection of the dashed circle and the diameter (the point that is very close to point C here); Other variations include constructing the perpendicular bisector of the segment where the segment is drawn from the center of the other circle (B, here) to the appropriate initial random point. Obviously, one sees the number of possiblilites that are generated.
After a tangent circle is constructed, the center is traced. This trace produces a locus of points that form an ellipse - for the constructions noted above. See the next picture.
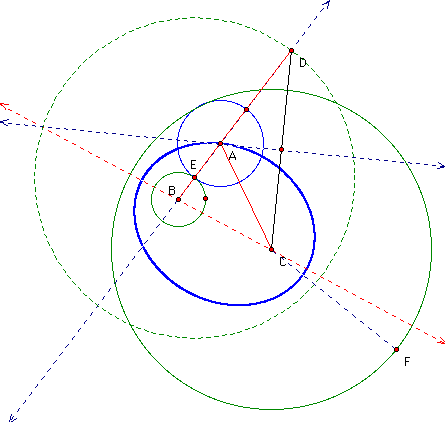
The locus of points of the trace of the center of the tangent circle is the thick blue ellipse in the following picture. The center of the tangent circle A is point A. Note the isosceles triangle with the black base (CD), and red-colored legs (AD, AC). Point A lies on the perpendicular bisector of the base of the isosceles triangle. Up to this point, the loci of the centers of the tangent circles constructed are ellipses. (Even though not all the possible constructions are shown).
This picture does not show the locus of the center of the tangent circle, but it does show the small green, given circle inside the blue tangent circle created by one of the constructions explained above. Here, the given point is on the smaller circle.

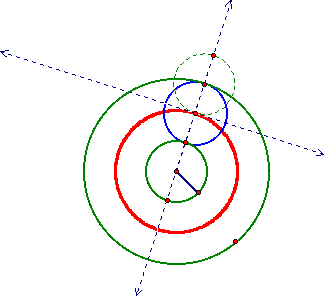
When the centers of the two green circles merge and the locus of the center of the tangent circle (blue) is observed, a special case of an ellipse occurs - a circle (red).
To this point, the two given circles (in green) do not intersect with each other. Now, consider what happens when they do:
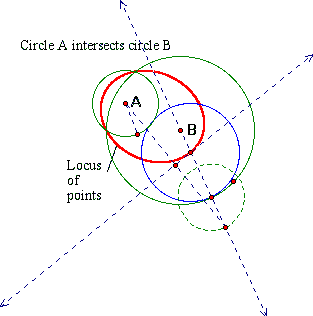
Circle A (small green circle) begins to exit the interior of the larger green circle (B). Here, the locus of points of the center of the blue tangent circle is an ellipse as usual. As Circle A moves farther away from the center of Circle B, the ellipse changes shape:
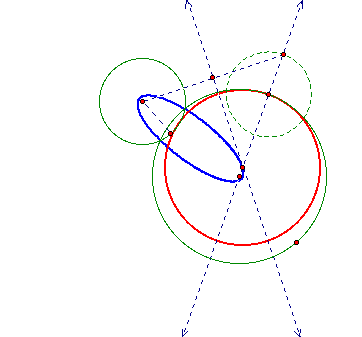
The blue ellipse has an eccentricity close to the value of 1 which makes it look flat. Remember, the ellipse is the locus of the center of the red tangent circle.
The loci of the centers of the tangent circles for all the cases that have been constructed are ellipses or a circle (a special ellipse). The following proof for the case where the constructed circle is exterior to the small given circle and where the given point is located on the small circle is the context. The remaining cases can be proved when using similar logic.
Proof of the locus of tangent circles:
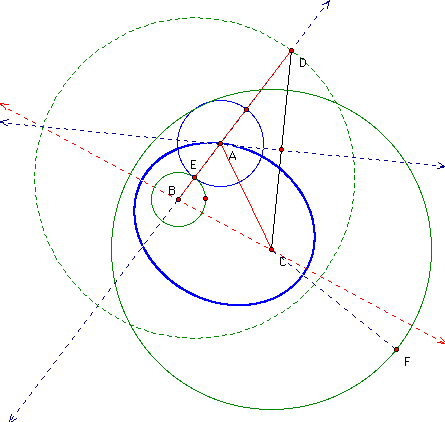
See figure. Segment BD is constant since it is the sum of the radii of circle C and circle B. Triangle ACD is isosceles because:
Point A lies on the perpendicular bisector of the midpoint of segment CD. Thus, segment AD = segment AC.
BD = BA + AD. Since AD = AC, by substitution, the length of BA + AC = BD which is constant. Then the set of all possible points A, forms an ellipse with foci B and C.
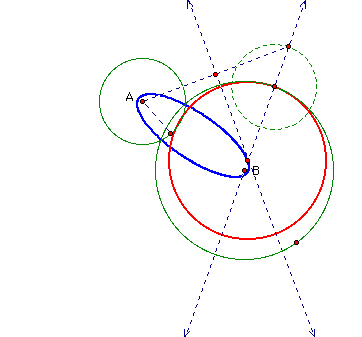
One interesting fact is that the red tangent circle never enters the region of intersection of circles A and B. This region is the small area bounded by two arcs; one arc from A and the other from B.
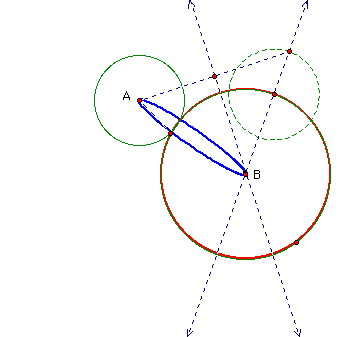
As circle A moves farther away from the center of B the two become tangent. At this point, it appears that the red tangent circle takes the same shape and size of circle B. The eccentricity of the ellipse approaches 1 and just at the point where A becomes disjoint from B, the conjecture is that the locus of points moves from an ellipse to a line connecting the centers. Immediately after, the locus disappears and then becomes a hyperbola. See the next two figures:
The next construction is that of two given (green) circles A and B, that lie outside of each other. Their centers comprise the foci of a conic whose locus is a hyperbola. This will be proven in a moment. The blue circle (C), is tangent to both circles A and B. Circle A is in the interior of the tangent circle C, while circle B is tangent to the outside of circle C. When the center of the interior circle, A, is traced, the resultant figure appears to be that of a hyperbola. As the trace continues in one direction far enough, the blue tangent circle "switches over" and circle B lies in the interior of C while circle A is exterior to the tangent circle. The trace of the center of circle B appears to be a hyperbola as circle C continues to move. The picture is the result of a single cycle where the blue circle "switched over " twice; encompassing circle A, encompassing circle B, then back to A again.
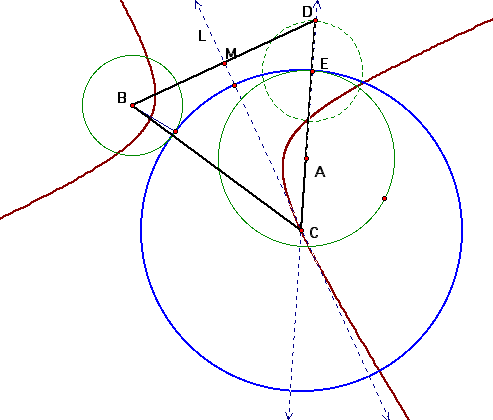
The proof for the hyperbola:
Given: Circles A and B; E is a point anywhere on one circle; segment BD; M is the midpoint of BD; By construction, line L is the perpendicular bisector of BD at M. Point C lies on the perpendicular bisector (line L) of BD. BC and CD have equivalent lengths, hence forming an isosceles triangle BCD.
Given: AD is the sum of the lengths of the radii of circles A and B, thus, AD is a positive constant.
Since Points A and B are centers of fixed circles, A and B are fixed points.
CD = CA + AD by construction;
BC = CD by fact of the isosceles triangle;
BC = CA + AD by substitution;
BC - CA = AD by subtraction;
Therefore, the locus of all points represented by C, the difference of whose distances (CA,CB) from two fixed points (A,B) is a positive constant. Points A and B are the foci. This is the definition of a hyperbola. (Analytic Geometry, by Protter-Morrey; Published by Addison-Wesley.)
The following is the trace of the tangent line rather than the center of the tangent line:

The trace of the tangent line produces an envelope (red) that sweeps out the hyperbola.
Next will be the consideration of the locus of the midpoint of the segment that formed the base of the key isosceles triangle in two conditions: The first where the one of the two given circles is interior to the other and second, where the two are disjoint.
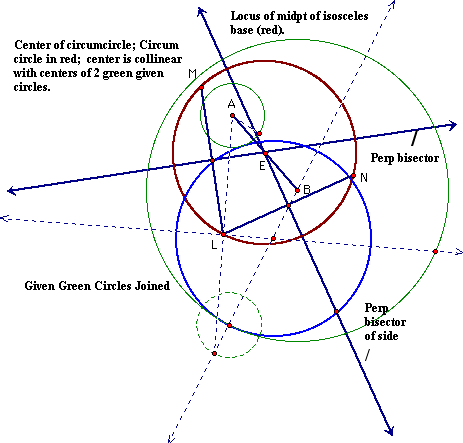
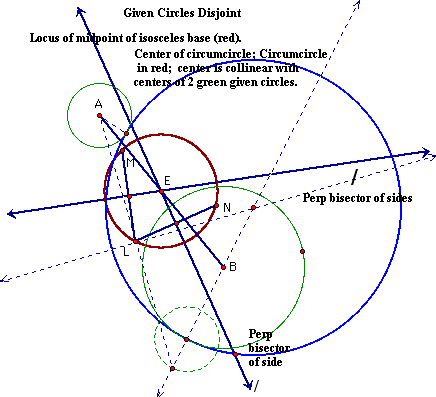
In both cases, the red circle,(E), is the locus of the midpoint of the base of the isosceles triangle. The center, E, is collinear with A and B, the centers of the given circles. To make things a little clearer, several objects have been hidden in the next picture:
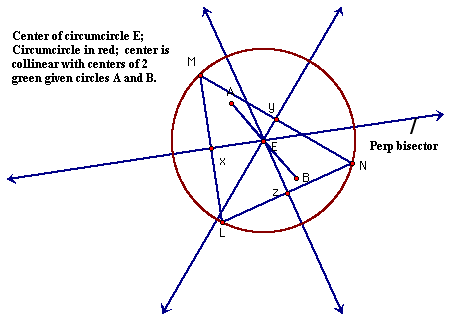
It is more apparent that point E is the center of a circumcircle about triangle LMN. LMN was formed and the respective midpoints x, y, z were used to construct perpendicular bisectors; These intersected at E. Again, E is collinear with A and B the centers of the two (hidden), green circles.
Much more could be investigated; this will be left up to the reader.