

This construction begins with creating any size triangle ABC and the orthocenters of ABC, HBC, HAB and HAC. Next, the circumcircles of each triangle are made:
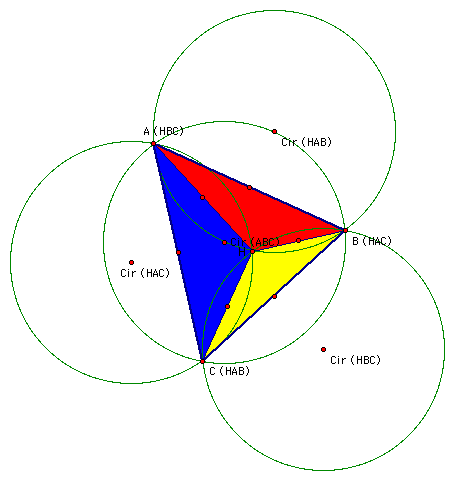
The labels may seem confusing, but, they are not. At point A there is a parentheses with HBC. This means that point A is the orthocenter for triangle HBC. Point B is the orthocenter for triangle HAC. Point C is the orthocenter for triangle HAB and , of course, H is the orthocenter for triangle ABC.
Further, the circle labeled (HAB) is the circumcircle for triangle HAB. The circle labeled (HBC) is the circumcircle for triangle HBC. Circle HAC is the circumcircle for triangle HAC and circle (ABC) is the circumcircle for triangle ABC.
By definition of a nine point circle: In any triangle, the midpoints of the sides, the feet of the altitudes, and the midpoint of the segments from the orthocenter to the vertices lie on a circle (A. Posamentier, Advanced Euclidean Geometry).
The following are the constructions of nine point circles for all four triangles. The first is for DABC. The next is for both ABC and HAB. Note that point N is the center of the nine point circle. Md = midpoint of the segment; alt is the altitude, H is the orthocenter.
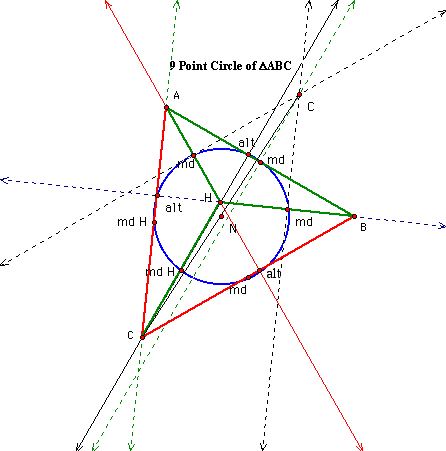
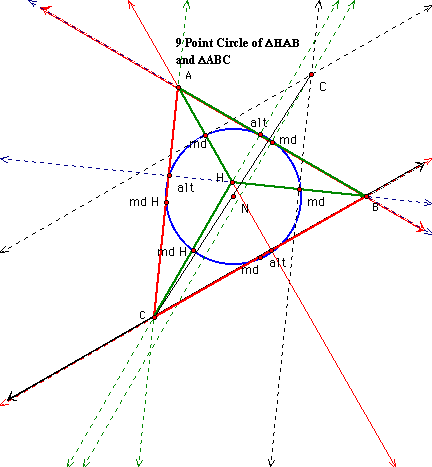
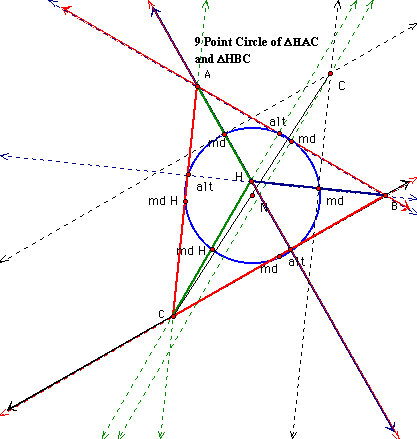
After the second and especially the third 9 point circle, it was evident that all four triangles share the same 9 point circle.
And now the proof that all four triangles share the same nine point circle:
Step one is to prove that the radii of the four circumcircles are congruent. The following figure shows the circumcircles with their radii highlighted:
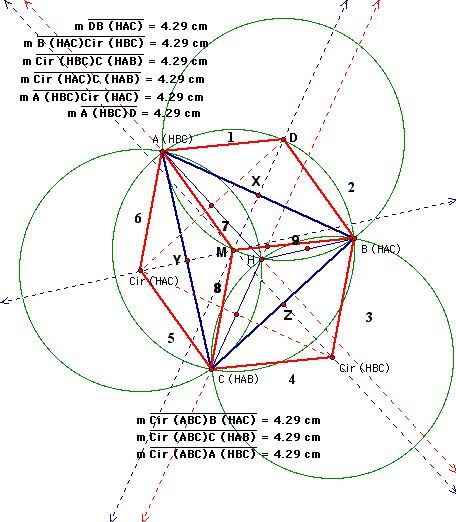
MD is the perpendicular bisector of AB at X, thus, length 1 = 2. AB is the perp. bisector of MD at X, so length 2 = 9 = 7. By similar reasoning, line MZ bisects CB at Z and CB bisects M-Cir(HBC), thus, length 3 = 4 = 9 = 8. Also, line MY bisects AC, thus, all 9 sides are equal. So, all the radii of the circumcircles are congruent.
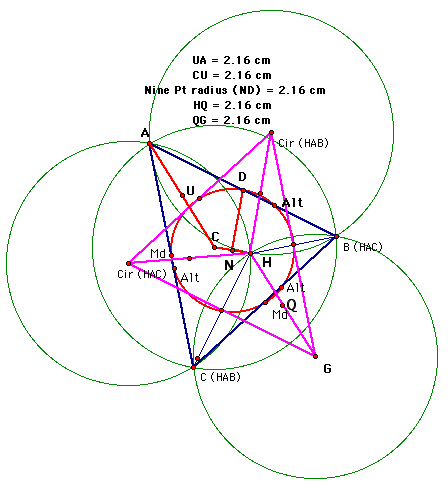
The next figure shows the red 9 point circle of DABC; triangle ABC in blue; and another series of triangles formed by the joining of the centers of the other three circumcircles, in pink.
The radius of the 9 point circle is given by ND. Segment AC is the radius of the center circumcircle. By construction we have: U is the midpoint of AC;Q is the midpoint of GH; Most important, ND - the radius of the 9 point circle is 1/2 the distance of the radii of the circumcircles: ND = UA = CU = HQ = GQ, etc. This is true for all of the circumradii.
By construction, N is the midpoint of the Euler line (segment) CH. It is also the center (again) of the 9 point circle. In the next figure, the Euler lines of all four circumcircles are shown in black for the outside three:
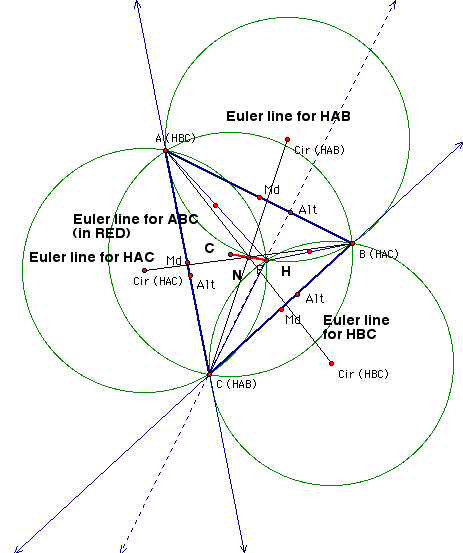
The midpoint of all the Euler lines is the fixed point N (by construction). Therefore, since all of the original triangles within and including ABC have the same fixed center (N), the fact that N is the midpoint of the Euler line in all cases, the fact that the radius of the 9 point circle is congruent to 1/2 of all the circumradii, and the fact that all the circumradii are congruent shows that the four original triangles have the identical 9 point circle.