A pedal triangle is formed by the following:
1) Construct a triangle and label it ABC.
2) Let there be a point P in any area of the plane.
3) Point P is called the Pedal point.
4) Construct perpendiculars to the sides of ABC.
5) Locate the three points that are the intersections.
These three points create a triangle called the Pedal triangle. See picture:
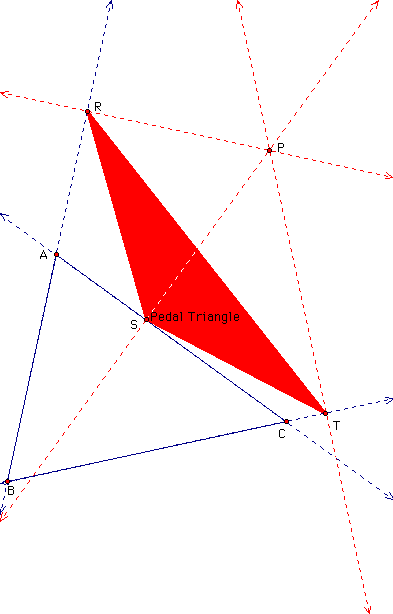
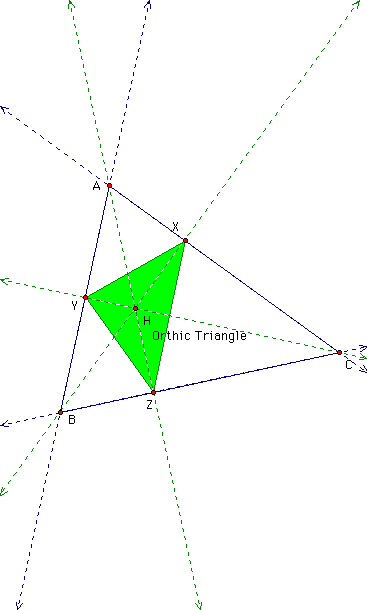
The initial triangle is ABC. The pedal triangle is RST. Point P is the pedal point. What happens if the pedal point becomes merged with a special point called the orthocenter H, of the orthic triangle? First, an orthic triangle (xyz), is constructed along with the ortho center H:
The next construction is both the pedal and orthic triangles together:
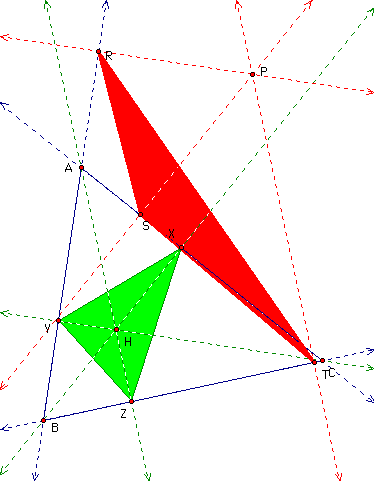
Next, the pedal point P will be merged into the orthocenter H:
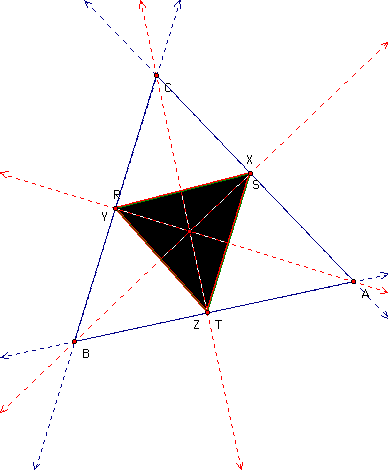
By observation, it appears that the three triangles formed by the orthic triangle seem similar to the original triangle. To restate it, triangles BTR, STA, and CRS are each similar to triangle BCA.
Proof: We will prove that DABC ~ D'sRSC, BRT and SAT. (Thanks to A. Posamentier, Advanced Euclidean Geometry). First is the proof for DRSC:
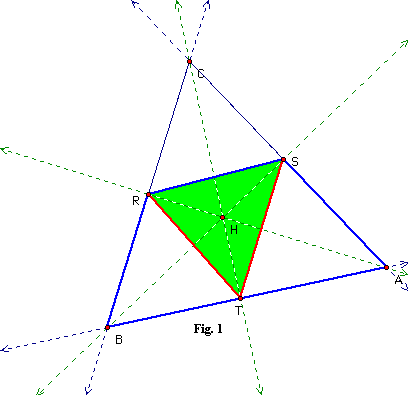
Quadrilateral BRSA is cyclic because < BRA and <BSA are right angles. Therefore <RBA is supplementary to <RSA (opposite angles of a cyclic quadrilateral). However, <RSC is also supplementary to <RSA. Therefore, <RBA is congruent to <RSC. Thus D ABC ~ DRSC (because both triangles also share <RCS).
For the next part of the proof DABC ~ DBRT, see figure 2:
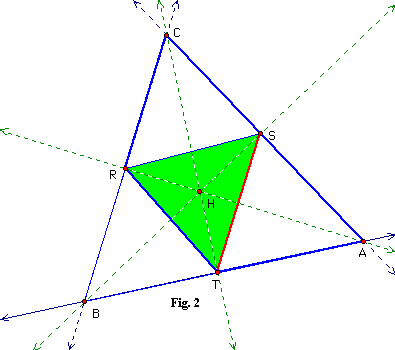
Quadrilateral RCAT is cyclic because <CRA and <CTA are right angles. Therefore, <TAC is supplementary to <TRC (opposite angles of a cyclic quadrilateral). However, <TRB is also supplementary to <TRC. Therefore, <TAC is congruent to <TRB. Thus, DABC ~ DTRB (b/c both triangles also share <TBR).
See fig. 3 for the proof of DABC ~ DSAT:
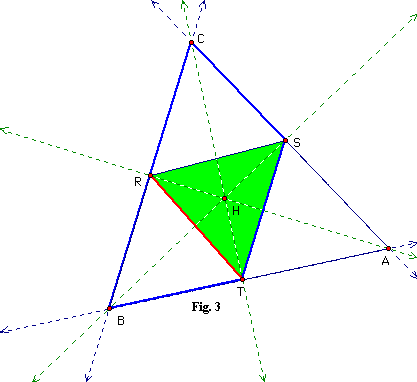
Quadrilateral STBC is cyclic because <CSB and <CTB are right angles. Therefore, <TBC is supplementary to <TSC (opposite angles of a cyclic quadrilateral). However, <TSC is also supplementary to <TSA. Therefore, <TBR is congruent to <TSA. Thus, DABC ~ DTSA (b/c both triangles also share <SAT).
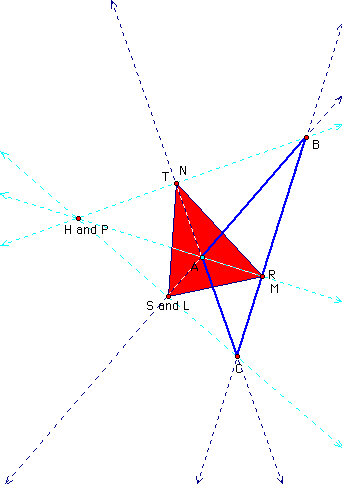
When the orthocenter and the pedal point are outside DABC they look like thus:
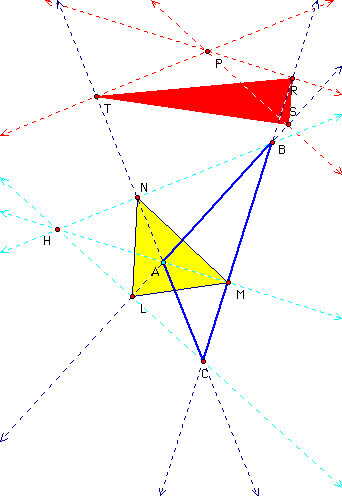
When the pedal point (P) is merged with the orthocenter (H), the following occurs: