Before I begin, I want to give credit to A.S. Posamentier for his great work Advanced Euclidean Geometry from which this essay gets its material.
How not to do geometric proofs. That should be easy, at least for me it is when 'doing proofs' doesn't come naturally. It is easy to make incorrect proofs when the accompanying pictures are drawn wrong. A fallacy is making believable arguments using false or invalid inferences, arguments or evidence. Sometimes it's difficult to see our invalid reasoning but hopefully you will be able to find any mistakes in the following reasoning.
Hopefully, you will see the use of reductio ad absurdum (R.A.A.) which is latin for: the disproof of a proposition by showing an absurdity to which it leads when carried to its logical conclusion.
For our first fallacious proof, we have:
Remember, scalene means to have three sides of a triangle of unequal length, and, isosceles means to have two sides of a triangle having equal length. So, this statement, put simply, is three sides of unequal length of a triangle (scalene), will always have two equal sides.
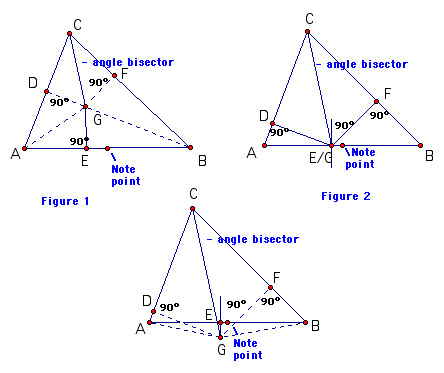
To prove that scalene triangle ABC is isosceles, draw the bisector of angle C and the perpendicular bisector of AB. From their point of intersection, G, draw perpendiculars to lines AC and CB, meeting these sides at points D and F, respectively. It should be noted that there are four possibilities for the above description for various scalene triangles:
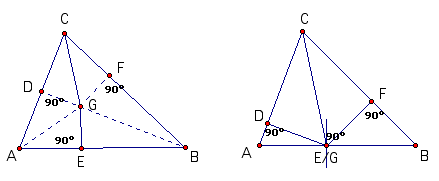
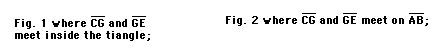
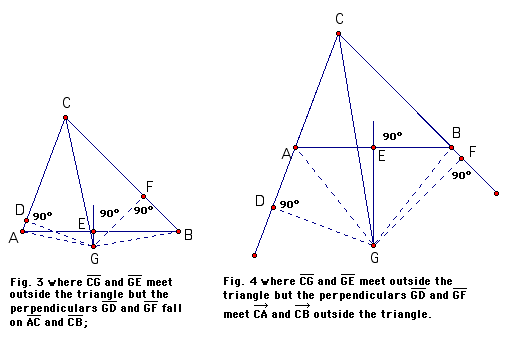
The proof of the fallacy can be done with any of these figures. Follow the 'proof' on any (or all) of the figures.
'Proof': Because Angle ACG is congruent to Angle BCG and right angle CDG is congruent to right angle CFG, Triangle CDG is congruent to Triangle CFG (SAA). Therefore, DG = FG and CD = CF. Because AG = BG (a point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment) and Angle ADG and Angle BFG are right angles, Triangle DAG is congruent to Triangle FBG (hypotenuse - leg). Therefore DA = FB. It then follows that AC = BC (by addition in Figures 1,2 and 3, and by subtraction in figure 4).
If you perform this construction correctly, you will see two properties in this type of situation:
1) The point G must be outside the triangle.
2) When perpendiculars meet the sides of the triangle, one will meet a side between the vertices, while the other will not.
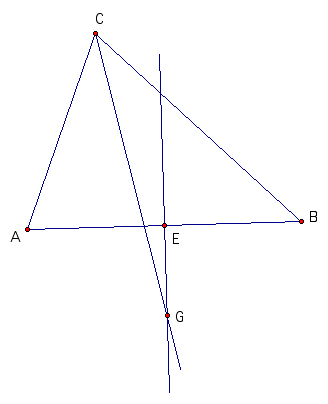
The following construction accurately reflects
the angle bisector of Angle ACB and the perpendicular bisector
of AB. If one manipulates the point of intersection of the two
bisectors, one will find that:
Figure 1 and 2 above cannot be constructed and properties 1 and
2 above will occur.