

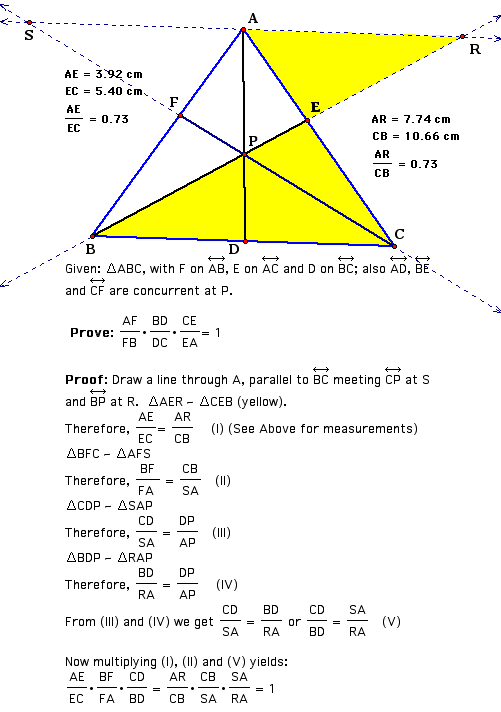
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in poins D, E and F respectively.
Explore (AF)(BD)(CE) and (FB)(DC)(EA) for various triangles and various locations of P.
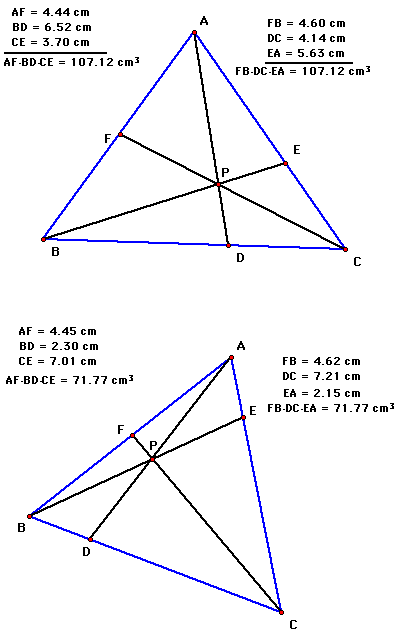
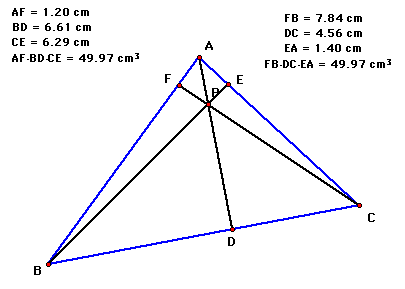
First, consider the ratio (AF)(BD)(CE)/(BF)(CD)(AE). According to the calculations, this ratio equals 1 everytime. This seems to be the conjecture. Proof? (This author gives is indebted to A. Posamentier, Teaching Secondary Mathematics, 5th ed. for help with this proof).

Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?
In the following figure, by observation, if one could move point P, the figure would show that the ratio of the areas never falls below the value of 4:
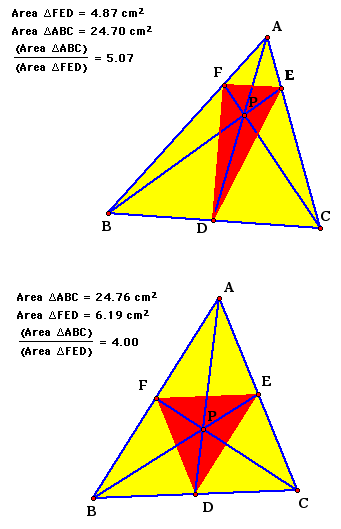
The smallest ratio is when P is the centroid.
From assignment 4 we see that with the centroid, all of the areas of the six triangles are equal.
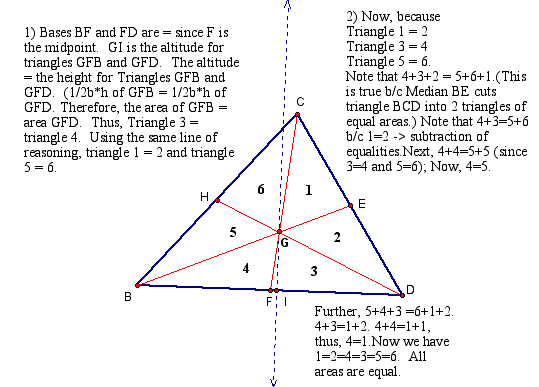
Further, the area of triangle EFH is 1/4th the area of BCD. Therefore, it holds that the smallest ratio of the areas of the two triangles is 4 units squared at the centroid and for all other points, the ratio of the areas is greater than 4 units squared.