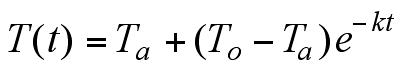
Today, we'll be investigating the rate at which boiling water cools in a cup of water
First we'll need to examine Newton's Law of Cooling
Newton's Law of Cooling says that the rate of change of the
temperature of an object is proportional to the difference between
its own temperature and the ambient
temperature (i.e. the temperature of its surroundings).
Newton's Law makes a statement about an instantaneous rate of change of the temperature. The solution to this equation will then be a function that tracks the complete record of the temperature over time.
Newton's Law of Cooling is given by the following:
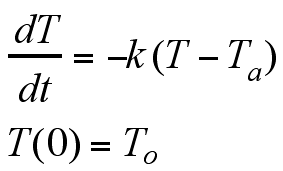
After some calculus, this yields the following equation:
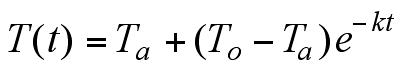
Where:

Table 1. Shows the temperature of boiling water as it cools in a cup of water. The initial temperature is the boiling state at time=0. Each minute (from 0 to 30) the temperature of the water was measured. We have different 31 measurements. Ambient temperature = 71 deg. Initial Temperature of the water =212 deg
| Time | Temp |
| 0 | 212 |
| 1 | 207 |
| 2 | 202 |
| 3 | 198 |
| 4 | 194 |
| 5 | 189 |
| 6 | 185 |
| 7 | 180 |
| 8 | 176 |
| 9 | 173 |
| 10 | 169 |
| 11 | 166 |
| 12 | 162 |
| 13 | 159 |
| 14 | 156 |
| 15 | 153 |
| 16 | 151 |
| 17 | 150 |
| 18 | 148 |
| 19 | 146 |
| 20 | 144 |
| 21 | 141 |
| 22 | 140 |
| 23 | 139 |
| 24 | 137 |
| 25 | 135 |
| 26 | 133 |
| 27 | 132 |
| 28 | 131 |
| 29 | 130 |
| 30 | 129 |
Now we use Newton's Law of Cooling to find an equation to model our data. I took time=12 and time = 24 to find k in Newton's Equation. I averaged the two values for k.
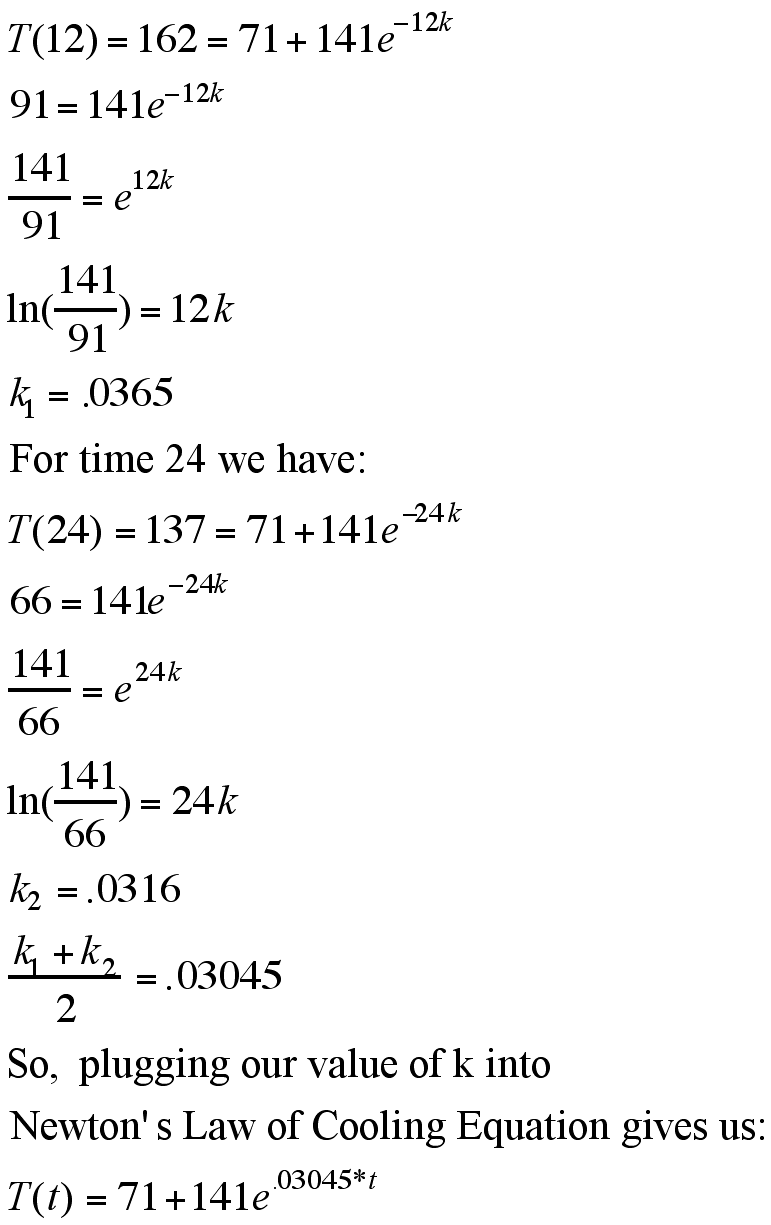
Table 2 gives us the model temperature, the squared differences between the observed data and the predicted values, and the sum of squares divided by the number of observations
| Time | Temp | Model Temp | Model - Obs | squared diff | |
| 0 | 212 | 212 | 0 | 0 | |
| 1 | 207 | 207.279767995136 | -0.279767995136126 | 0.0782701311024874 | |
| 2 | 202 | 202.717554360341 | -0.717554360341353 | 0.514884260044888 | |
| 3 | 198 | 198.308069142653 | -0.30806914265284 | 0.0949065966548561 | |
| 4 | 194 | 194.046199479925 | -0.0461994799253773 | 0.00213439194537534 | |
| 5 | 189 | 189.927003672393 | -0.927003672393425 | 0.859335808630897 | |
| 6 | 185 | 185.945705452698 | -0.945705452698405 | 0.894358803263496 | |
| 7 | 180 | 182.097688447738 | -2.09768844773754 | 4.40029682377153 | |
| 8 | 176 | 178.378490825912 | -2.37849082591197 | 5.65721860894739 | |
| 9 | 173 | 174.783800123568 | -1.78380012356837 | 3.18194288084253 | |
| 10 | 169 | 171.309448244635 | -2.30944824463458 | 5.33355119464575 | |
| 11 | 166 | 167.951406627652 | -1.95140662765189 | 3.80798782644373 | |
| 12 | 162 | 164.705781574599 | -2.70578157459931 | 7.32125392944114 | |
| 13 | 159 | 161.568809736094 | -2.56880973609429 | 6.59878346025284 | |
| 14 | 156 | 158.536853747734 | -2.53685374773445 | 6.43562693739435 | |
| 15 | 153 | 155.606398012521 | -2.60639801252069 | 6.79331059967178 | |
| 16 | 151 | 152.774044624471 | -1.77404462447137 | 3.14723432961577 | |
| 17 | 150 | 150.036509428701 | -0.03650942870118 | 0.00133293838408655 | |
| 18 | 148 | 147.390618213396 | 0.609381786604359 | 0.371346161845121 | |
| 19 | 146 | 144.833303029267 | 1.16669697073348 | 1.36118182151869 | |
| 20 | 144 | 142.36159863222 | 1.63840136777998 | 2.6843590419433 | |
| 21 | 141 | 139.972639045113 | 1.02736095488675 | 1.05547053162581 | |
| 22 | 140 | 137.663654234612 | 2.33634576538793 | 5.45851153544612 | |
| 23 | 139 | 135.431966899297 | 3.56803310070279 | 12.7308602077108 | |
| 24 | 137 | 133.274989365294 | 3.72501063470554 | 13.8757042286694 | |
| 25 | 135 | 131.190220585829 | 3.80977941417095 | 14.5144191846407 | |
| 26 | 133 | 129.175243241226 | 3.82475675877413 | 14.6287642637884 | |
| 27 | 132 | 127.227720935992 | 4.77227906400798 | 22.7746474647688 | |
| 28 | 131 | 125.345395489732 | 5.65460451026772 | 31.97455216754 | |
| 29 | 130 | 123.526084318756 | 6.47391568124374 | 41.9115842478536 | |
| 30 | 129 | 121.767677905341 | 7.23232209465914 | 52.3064828808948 | |
| 270.770313259298 | sum of squares | ||||
| 8.73452623417091 | sum of squares/31 |
Using our function we predict the temperature after 45 minutes, 60 minutes, or 300 minutes:
| 45 | 101.462910376104 | |
| 60 | 89.2791285099322 | |
| 300 | 71.0051629863876 |
We see that at time = 300 minutes our water has cooled to the initial room temperature! Sweet!
To refine our model we could calculate new k values use different times. Say when t=10 and t=20 we can compute another Newton's Cooling Equation with the new k value. By comparing the sum of squares (divided by the number of data points) for both our models, we can see which one is a better fit! A better fit is determined by a lower sum of squares.
References:
www.ugrad.math.ubc.ca/coursedoc/math100/notes/diffeqs/cool.html
Sarah Ledford, University of Georgia, Department of Mathematics Education