The Parabola: Mystery Solved!

While you slept through class, you may have missed some key points about the parabola. I know your rest is important, so I'll review some terms we "need" to know. Note: the term "need" is always relative. All we really need is to be happy. Given this tangent, let us review:

A focus is just an arbitrary point.

A directrix is just an arbitrary line.

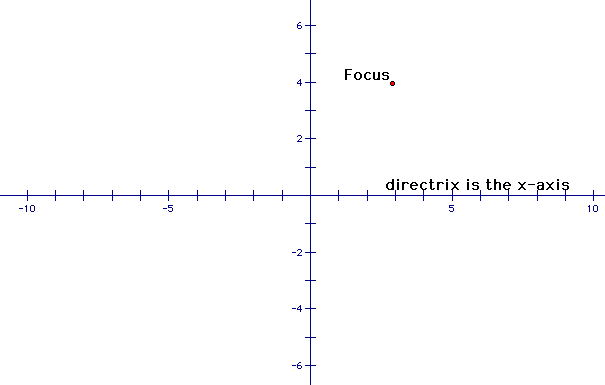
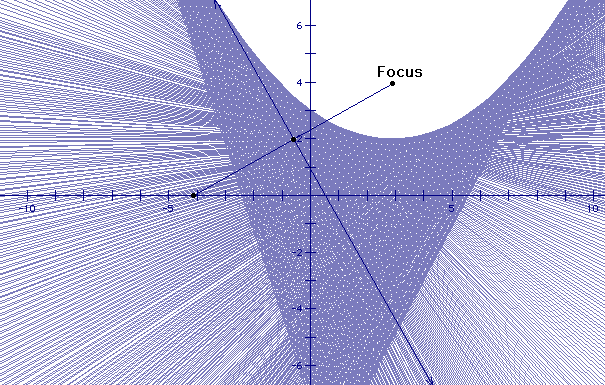
Let us expound graphically! Our focus is just a point we choose and we'll let the a-axis be our directrix.

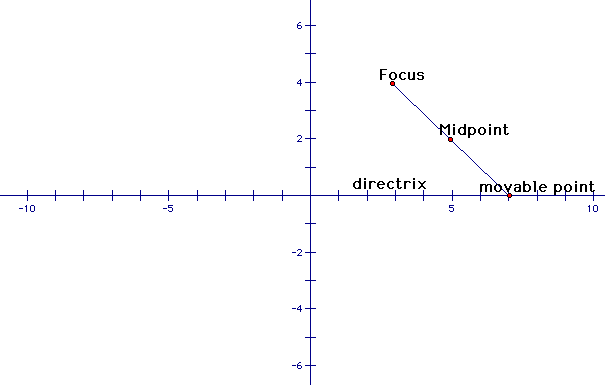
Next, we'll place a movable point on our directrix, draw a segment from our focus to the movable point, and find the midpoint of the segment.

Draw a line perpendicular bisector through the mid point!

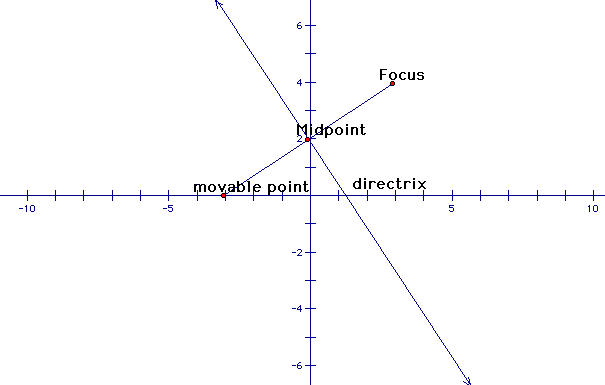
Next, we'll move the movable point back and forth across the directrix (the x-axis in our example). Do you see something? Looks like a parabola!

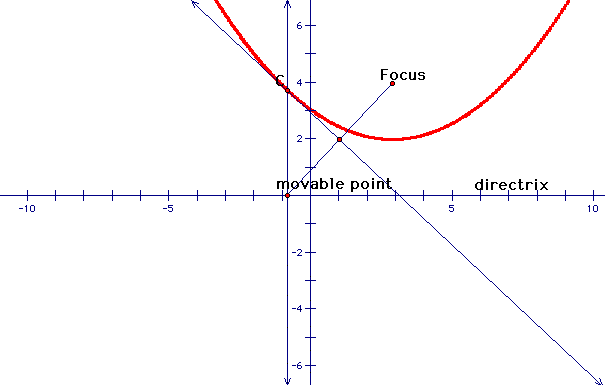
Let's get back to our picture...we know that perpendicular lines form 90 degree angles...

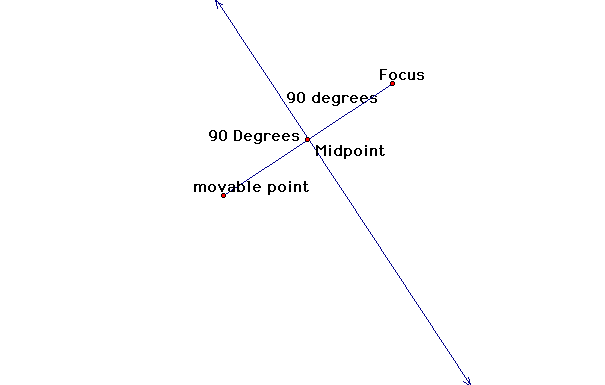
So a perpendicular line m form the movable point of the directrix will give an intersection at C. The line segment m will be equal to the line segment L.Do you know why? It has something to do with the angles being equal. The point C is where the distance from the focus and the directrix are the same...giving us one point that lies on the parabola.

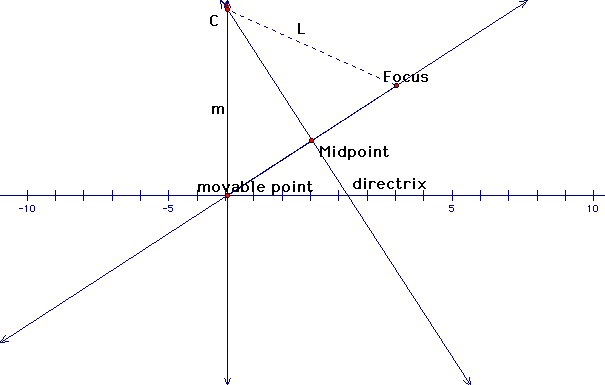
The locus of points in a plane whose distances from a focus and a directrix are equal will give us a parabola!

By moving out movable point across the directrix the point C also moves which forms the locus of points that make the parabola!