Prologue:
Let's look at a few concepts that you may not be familiar with...

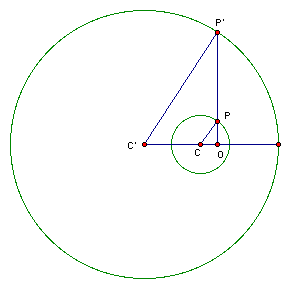
1)The radius C'P' is parallel to radius CP
2) P'P cuts C'C at a fixed point O
3) The fixed point O divides C'C externally in the ratio of the radii of the two circles
Finally: This is the external center of similitude
Internal center of similitude
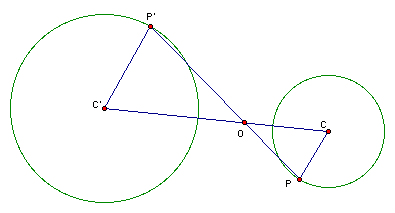
1) The radius C'P' is parallel to radius CP
2) P'P cuts C'C at a fixed point O
3)The fixed point O divides C'C internally in the ratio of the radii of the two circles
Yes, This is the internal center of similitude
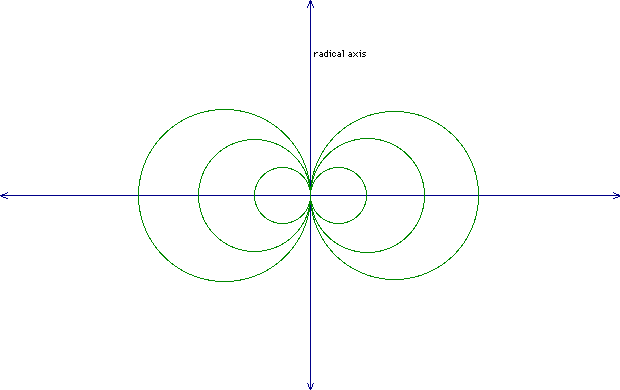
Radical Axis
The radical axis is where the circles touch on the y-axis
Now, we'll see how they are related:
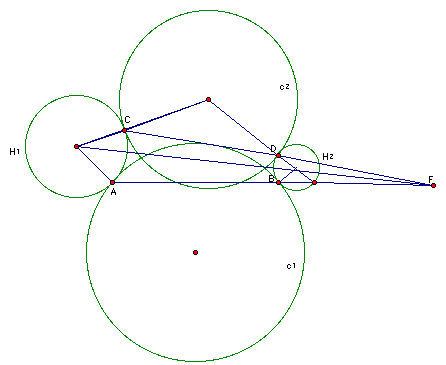
(i) If two non-concentric circle H1 and H2, touch to other non-concentric circles at A,B and C,D respectively, and if AB and CD are either both external or both internal centers of similitude, then AB and CD meet in a center of similitude of the circle H1,H2, or they are parallel to the line of center of these circles.
Using the Thm of Menelaus (for more info on the Thm. of Menelaus check out: http://jwilson.coe.uga.edu/emt725/Menelaus/Menelaus.html), we find where AB cuts the line joining the centers of H1,H2, and we consider the triangle formed by the centers of H1,H2 and C2, we see that CD passes through the same point F, and this point is the center of similitude of H1 and H2.
(ii) Note that FA x XB =XC x XD, so that is on the radical axis of C1 and C2.
Therefore AC and BD meet at a center of similitude of C1 and C and this center is on the radical axis of H1,H2
So, the radical axis of C1 and C2 contains a center of similitude of H1 and H2, and the radical axis of H1 and H2 contain a center of similitude of C1 and C2.
The End!
*adapted from the book Circles By D. Pedoe pages12-22