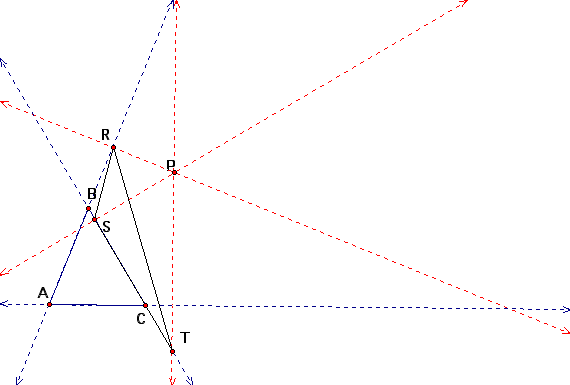
What is a Pedal Triangle?
Let's examine the construction of a pedal triangle. Starting with the triangle ABC we let P be a point outside of our given triangle. Next we draw perpendicular lines form the point P to each side of the triangle ABC. Labeling the points R,S, and T where the perpendicular lines intersect the extended lines of triangle ABC gives us our pedal triangle RST.

Cleaning up our picture a bit gives us a more lucid view of pedal triangle RST and pedal point P
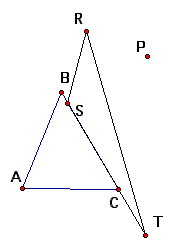
In order to find the area of the Pedal Triangle we need to look at the concept of Trilinear Coordinates.
From the website www.mathworld.com we know that the trilinear coordinates of a point P with respect to triangle ABC are an ordered triple of numbers, each of which is proportional to a directed distance from P to one of the side lines. Trilinear coordinates are denoted Alpha:Beta:Gamma.

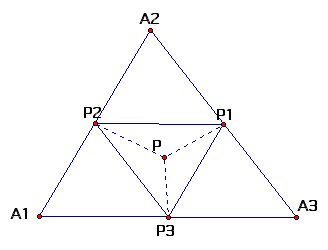
Using trilinear coordinates, the three vertices A,B,C are given 1:0:0, 0:1:0, and 0:0:1. Let the point in the above diagram have trilinear coordinates alpha:beta:gamma and lie at the distances a',b',c' from the sides BC,AC, and AB respectively.
Now, on with the show! I'm a lover, not a mathematician but I'm doing the best I can!
Let's find the area our the Pedal Triangle.
Given a point P, the pedal triangle of P is the triangle whose vertices are the feet of the perpendiculars from P to the side line.
The pedal triangle of a triangle with trilinear coordinates alpha:beta:gamma and angles A,B, and C has vertices with trilinear coordinates (www.mathworld.com):
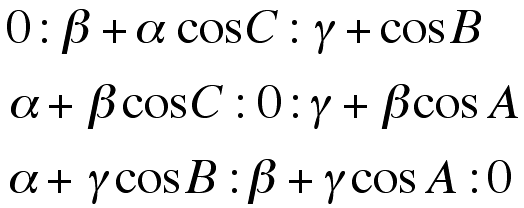
The area of A of the pedal triangle of a point P is proportional to the power of P with respect to the circumcircles:
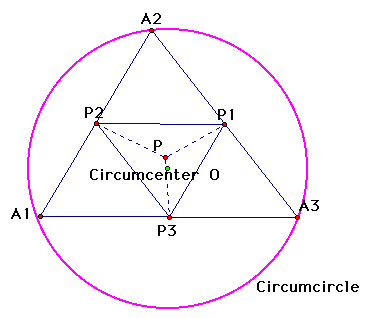
So, the area of the pedal triangle A is given by:
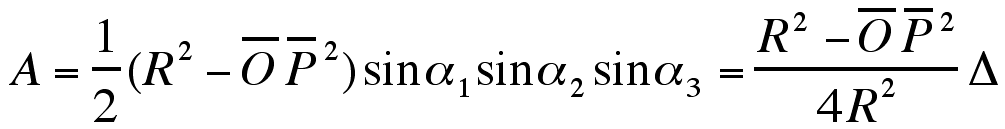
Extension: Prove it! You
say?
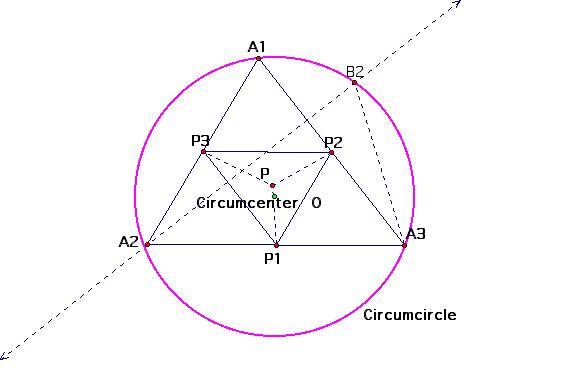
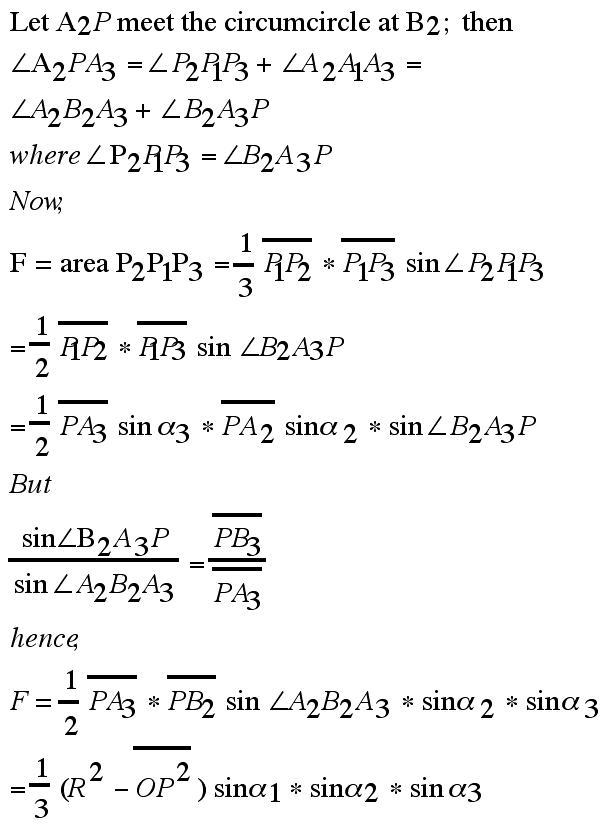
Wow...I need a nap!
References:
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, 1929.
www.mathworld.com