Assignment # 2

Fall 2002 Semester

Second Degree Equation

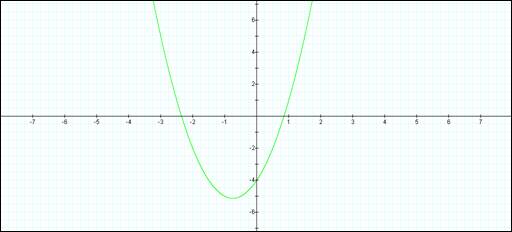
Problem 2- 6 :  Graph

y = 2x² + 3x - 4

i.      Overlay a new graph replacing each x with (x – 4).

ii.      Change the equation to move the graph into the second quadrant.

iii.    Change the equation to produce a graph concave down that shares the same vertex.

The above graph is the representation for the initial equation: y = 2x² + 3x -4.

There is one y-intercept point (when x = 0) of -4.  There are 2 solutions for x (when y =0) of ~0.85 and ~-2.35.

The vertex of the parabola created, is determined to be at x = -0.75 and y = -5.125.

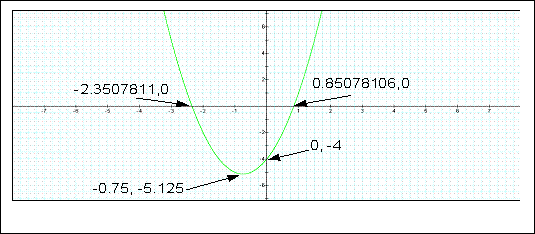
i.       Overlay a new graph replacing each x with (x – 4).  

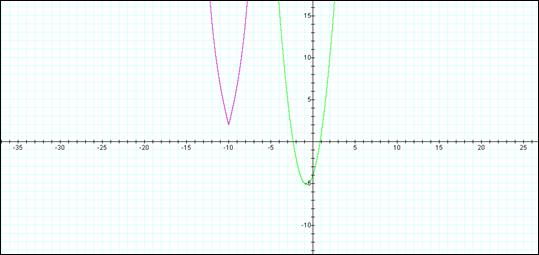
Graph of overlay of initial equation with equation replacing x by x -4.  The equations plotted are:

2x² + 3x -4 (Green)

and

2(x-4)² + 3(x-4) -4 (Red)

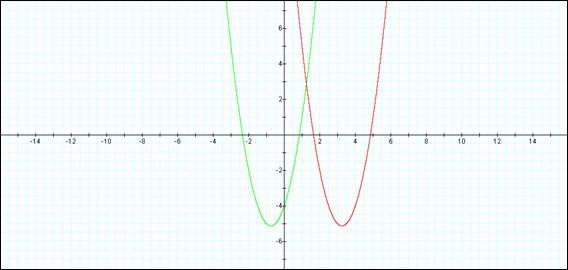
The net affect of changing from “x” to “x-4” is to shift the parabola further up the x-axis.   All of the x parameter items from the initial graph are increased by 4.  e.g. the vertex of the parabola is now at x = 3.25, y = 5.125.

ii .  Moving the graph into the 2^nd quadrant

The problem here is to adjust the parameters to provide a graph that appears in quadrant where:

y > 0

and

x < 0

From step i. it appears that all that 2 things need to be done:

1. Shift the parabola to the left by using “x+n” where the value of n will allow the parabola to be far enough left to allow for the plot not to cross the y-axis.
2. Change the vertex point for “y” by increasing the intercept parameter e.g. -4 to +1\2

e.g. y = 2(x+100)² + 3(x+100) + 2

However, it appears that this will not work, as any increase in the value of n will eventually cross the y-axis (although usually at some point well beyond where we’re able to plot.  For the purposes of demonstration, it appears to be within quadrant 2.

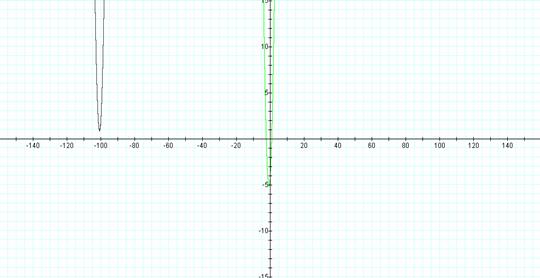
The graph below changed the equation to the following:

y = e^{|(-x) -10|} + 3(|-x-10|) + 1

This also appears to be within the 2^nd quadrant, however, as with the first, when y is large enough, there is an intersection with the y-axis (there is a solution for y when x is zero or positive.)

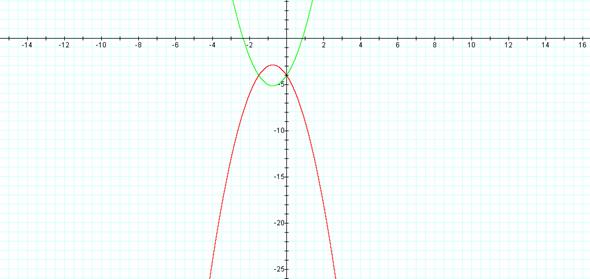
iii.    The following graph is the result of changing the equation to produce a graph concave down that shares the same vertex with the first equation.  The equations used are as follows:

 2x² + 3x -4 (Green)

-2x² - 3x -6.25 (Red)

The second equation was determined by:

·        Determining the vertex point of the original graph.

·        Inverting the original graph’s parabola.

·        Changing the y intercept parameter (-4) to match the inverted parabola.

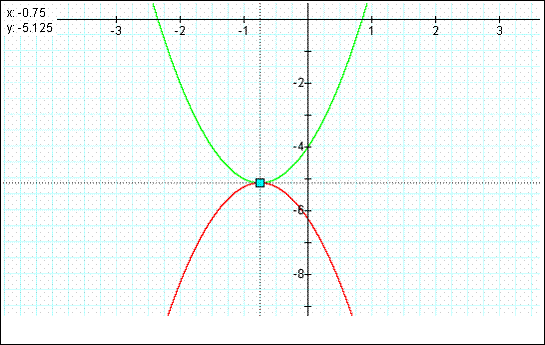
Vertex Point Determination:

1. From calculus, note that the minimum and maximum points may be determined from the first derivative of the equation.  The first derivative provides us with a linear equation that represents the slope of the curve at any of the points.  The minimums and maximums of the equation would be points where the slope would be zero.  i.e.

First derivative of:  y = 2x² + 3x – 4 yields ΰ y = 4x + 3. 

2. Next determine the value of “x” when y = 0:

When y = 0, the x = -0.75

3. Then calculate y for when x = -0.75

For y = 2x² + 3x – 4, when x = -0.75, then y = -5.125

Inverting the Parabola:

The parabola can be inverted, by changing the polarity of the x-parameter parts of the equation.  i.e. y = 2x² + 3x – 4 becomes -2x² - 3x – 4.   

This yields the graph below.  Still not finished.

Changing the y intercept parameter (-4) to match the inverted parabola:

The y intercept needs to be changed for the new parabola.  We determined the vertex point for the original graph to be at x = -0.75 and y = -5.125.    These same vertex points apply to the new calculation.  What is needed is to replace -4 by a variable name (e.g. “n”), and substitute the x and y values for the vertex (-0.75 and -5.125, respectively).

i.e.  -5.125 = -2(-0.75)² -3(-0.75) – n;  

n = 5.125 – 1.125 + 2.25 ΰ 6.25

The final equation becomes: -2x² - 3x - 6.25 

Return........