Assignment # 4
Fall 2002 Semester
GSP - General Figures
1.
Prove
that the three medians of a triangle are concurrent.
2.
Prove
that the centroid (the point of concurrence) is two-thirds (2/3) the distance
from each vertex to the opposite side.
4.
Show
how you can develop a “sense of proof” of the relationship with students.

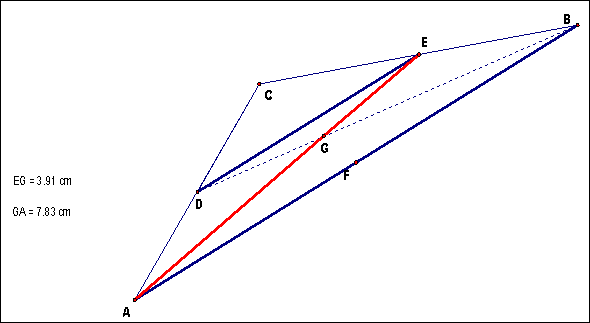
The
above diagram shows the basic construction of the triangle, the midpoints of
each side and the line segments between the vertices and the midpoints.
A
brief outline of the proof is as follows:
0. Verify that 2 of the line segments (vertex to midpoint) will intersect at some point G. (Crossbar Theorem and Prop 3.7 à Given an angle CAB and point D lying on line BC, then D is in the interior of CAB iff B*D*C)
1. Construct the line segment FE – then show that this segment is:
a. Parallel to AC.
b. ½ the length of segment AC
Both of these fall out of the proof that ∆ABC is similar to ∆FBE.
2. Construct the line segments AE and FC and the intersection point “G” – then show that:
a. Line segment GE is ½ the length of segment AG
b. Line segment GF is ½ the length of segment CG
Both of these fall out of the proof that ∆AGC is similar to ∆EGF
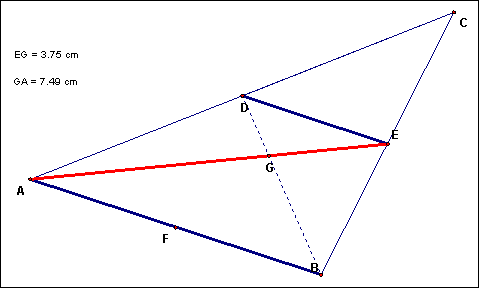
3. Remove the construction of line segments FE and FC. Construct the line segment ED – then show (as in #1 above):
a. Parallel to BA.
b. ½ the length of segment BA
Both of these fall out of the proof that ∆ABC is similar to ∆DEC.
4. Construct the line segment BD and the intersection point “G1” – then show that:
a. Line segment G1E is ½ the length of segment AG1
b. Line segment DG1 is ½ the length of segment G1B
Both of these fall out of the proof that ∆AG1C is similar to ∆EG1F
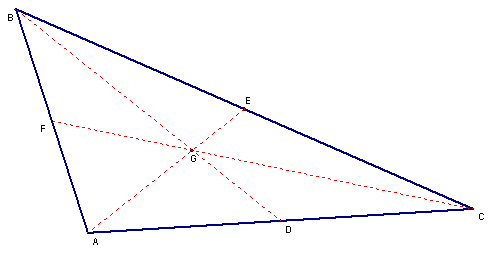
5. We now have:
Line segment G1E is ½ the length of segment AG1, and
Line segment GE is ½ the length of segment AG
Knowing that both G1 and G are on the same line segment (AE), and both points are at the same distance from A and E as each other,
then G1 = G. I.e. all 3 lines are concurrent (at point G).
Back to beginning, with a little more detail on the key items….
Let’s start with the proof that any two of the lines (rays) that extend from the vertices of the triangle through the midpoints intersect.
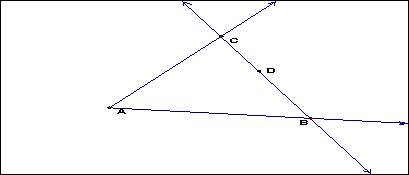
Two basic theorems allow us to make the claim that if we have any two rays that extend from any two vertices of the same triangle that these two rays will intersect at a point in the interior of the triangle. The intersection part of the above is proven by looking at the Crossbar Theorem. ( If ray AD is between ray AC and ray AC, then ray AD intersects segment BC.) This is illustrated below:

The interior part of the proof lies in the Prop. 3.7 quoted (Given an angle CAB and point D lying on lin BC, then D is in the interior of angle CAB if and only if B * D * C) This is illustrated below:
By
allowing the segments from the vertices to the midpoints create a secondary
triangle, it is easy to apply these theorems to verifying that there will be an
intersection within the interior of the triangle.
Next let’s look at two of these lines and their respective intersection.
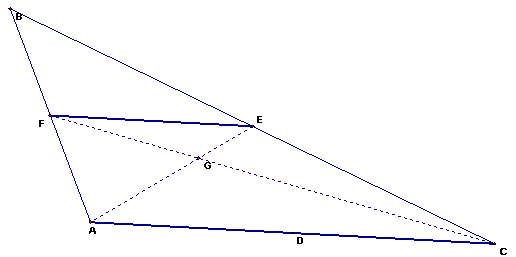
First, by constructing the line segment FE, we can note the following:
BF/BA = ½ (since F is the midpoint)
BE/BC = ½ (since E is the midpoint)
Angle FBE is congruent to Angle ABC
Therefore, ∆FBE is similar to ∆ABC by Side Similar/Angle Congruent/Side Similar
This means that FE is similar to AC by the same ½.
And Angle BFE is congruent to Angle BAC; Angle BEF is congruent to Angle BCA.
This leads to congruency between the alternate interior angles of line EF and line AC. By Alternate Interior Angle Theorem, we know that line BE is parallel to line AC.
That takes care of Step 1 of the outline.
Step 2 of the outline is similar. We want to show that the two triangles, ∆EGF is similar to ∆AGC.
We know that angle EGF is congruent to angle AGC (opposite angles)
We also know that angle AEF is congruent to angle EAC and angle EFC is congruent to angle ACF, since they are alternate interior angles to parallel lines EF and AC.
Therefore, ∆EGF is similar to ∆AGC.
We know that the length of one segment of ∆EGF (FE) is in a ratio of ½ to the similar segment of ∆AGC (AC). i.e. FE/AC = ½. Therefore the remaining segments of the two similar triangles are in the same ratio. EG/GA = ½ and FG/GC = ½.
Finally, let’s considerthe 3rd segment, from steps 3 and 4 above.
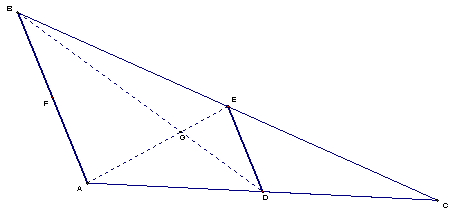
We now will take away two segments (FE and FC) to examine the third segment, BD. We will need to add the segment between the midpoints E and D (ED).
Following the same logic as above, we can see that ∆CED is similar to ∆CBA.
ED parallel to BA follows, as well as the ratio of length of ED to BA (½).
This brings us to the two triangles: ∆EGD and ∆AGB. By showing the similar congruence between angles of the two triangles, we can show they are similar triangles. This means that the ratio of the remaining sides are also in the same ratio of ED to BA (½).
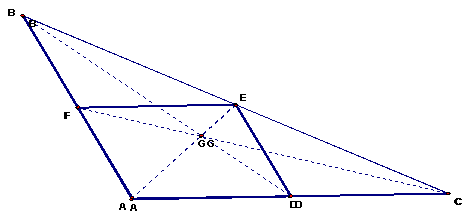
Finally, we come to step 5. In this last sketch, the two parts of the proof are overlaid to indicate that it looks like we have concurrence. Since we have the same ratio of ½ for the same set of lines (AG/GE = ½ for both cases) then G must be the same for both cases. Therefore the 3 lines are concurrent at point G.
This proof falls out immediately from the proof shown in #1 above. The line segment length ratios are the same for AG/GE, DG/BG, and FG/CG à ½.
Therefore the centroid (“G”) is ⅔ the distance from each vertex and ⅓ the distance from each midpoint.
GSP
can be used in a number of ways to help understand the relationships between the
triangle and its medians. One way,
in this proof, is by showing the various lines are parallel.
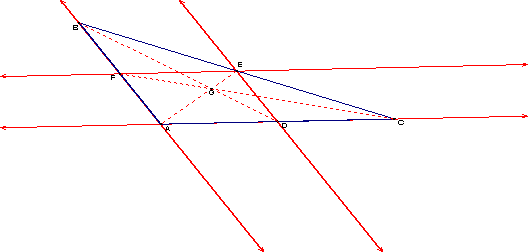
GSP can construct the parallel lines (bases and lines between the
midpoints) or the lines can be constructed that can immediately be suspected of
being parallel. The challenge then
remains in explaining /proving that the lines, indeed are parallel. See
the plot construction below:
Another
aid from GSP in the construction/de-construction of the various pieces (e.g. the
similar triangles) that allows for the objects to be superimposed to more
clearly show the relationships between apparently dissimilar objects. An
example is shown in the sketch below:
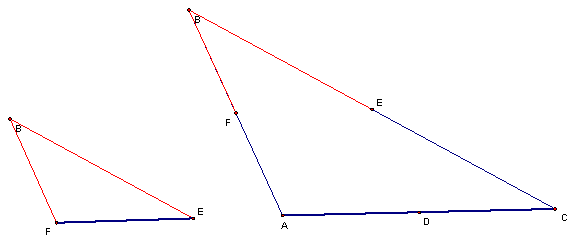
We
can superimpose the smaller ∆BFE onto the larger ∆BAC to see the
relationship between the triangles even more clearly. The
1:2 ratio of segment F1E1 to AC stands out in particular,
as well as the parallelism between lines B1E1 and BC.
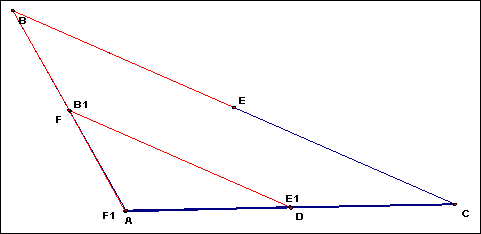
The “sense of proof” can be thought of as the changing of the actual object into an object that immediately shows what we are trying to prove. In the above proof, if we take the respective shorter line segments (the 1/3’s) and lay 2 copies end to end against the longer of the line segments (the 2/3’s), then it is obvious that there is a 2 to 1 ratio. We can further show this works for any triangle, by allowing the shape of the original triangle to change (while having the duplicated segments linked to this change) and see that indeed, for any triangle shape we create, the ratio stays the same.