Tangent Circles
Problem 7.1: Make a script tool for the construction of
tangent circles.
See the following GSP file, if you have Geometer’s Sketchpad.

Problem 7.2: Make a script tool for tangent circles within
each other.
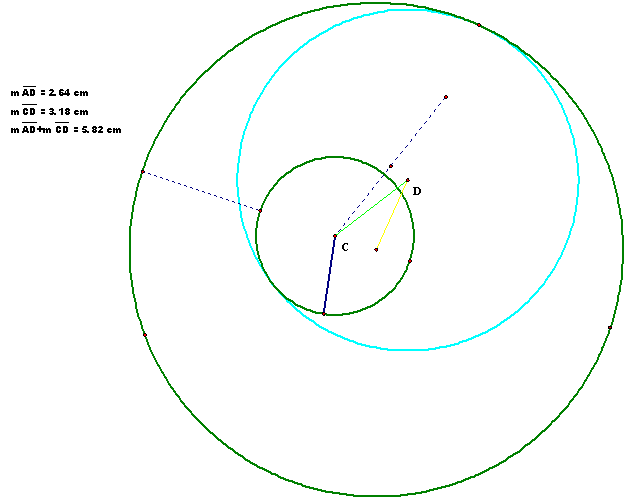
Problem 7.3: Construct the tangent circle to 2 given
circles. The given point is on the
smaller of the two circles – 2 cases:
1. Smaller circle is external to
the tangent circle.

First sketch shows the point on the larger circle, the second shows the point on the smaller
circle.
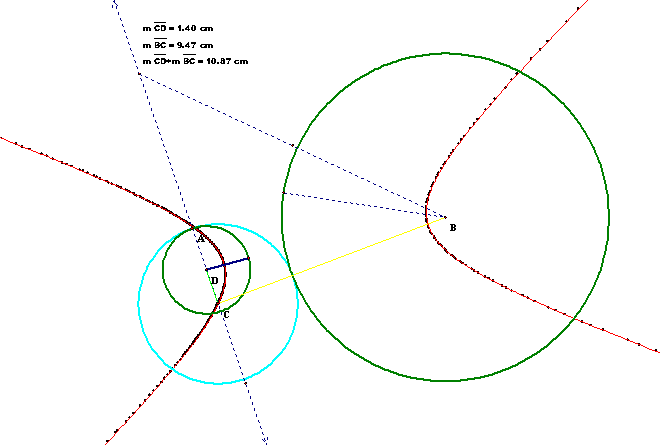
2. Smaller circle is internal to
the tangent circle.
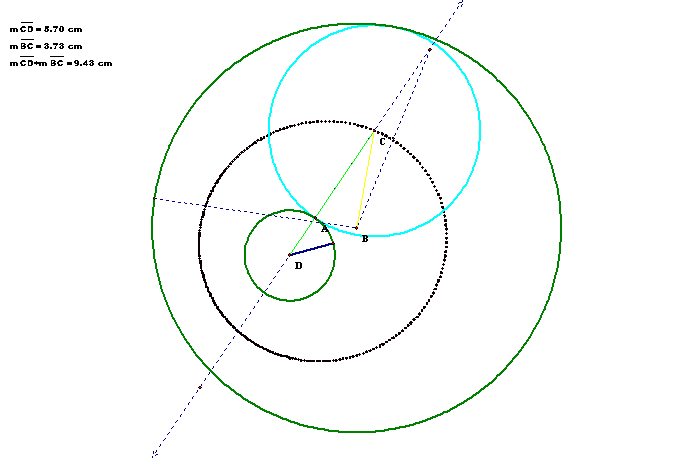
Problem 7.4: Discuss the loci of the centers of the
tangent circles for 7.1 through 7.4.
All of the circles, to this point, have loci that appear to be
elliptical around the foci of each of the other tangent circles. This is shown in the constructions by noting
that the sum of the distance from the center of each of the given circles to
the center of the tangent circle is constant.
This basically defines the focal points of the ellipse as the centers of
the two given circles.
Problem 7.5: Discuss the construction of tangent circles,
if the given circles intersect.
When the two circles that are given are intersecting, the tangent
circle center traces a loci that appears to be elliptical around the two
centers of the given circles. The main
difference is that the circle reduces to a point as it crosses the intersection
of the 2 given circles. The tangent
circle is then interior to the second circle, and reduces to a point before it
returns to the first circle.
See the following progression:
Start with the tangent circle (green) within the larger circle.

Then note that the tangent circle decrease in size as it approaches the
smaller circle…

As the tangent circle reduces to a point at the intersection point and
the proceeds to be interior to the smaller circle and exterior to the larger
circle…
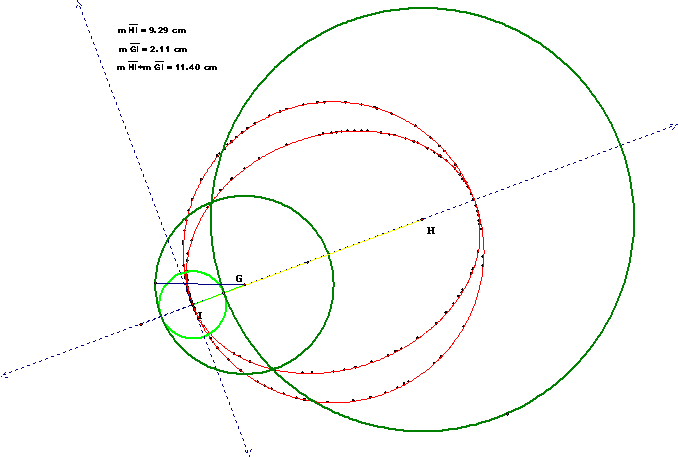
The tangent circle proceeds through the 2nd intersection
between the two circles and back interior to the larger circle.

One can also check to see how the locus of the center of the tangent
circle changes as the intersection of the two given circles goes from the two given
tangent with the smaller interior to the larger and then when the two given
circles are tangent, with the smaller being exterior to the larger:
Interior: The ellipse still
remains, but is closer to being circular.
The total length remains the same of the two segments between the
centers as in the previous, due to the size of the circles remaining the
same. The tangent circle doesn’t appear
in the interior of the smaller circle, but is reduced to a point at the point
of tangency.

Exterior: Again, the total
length between centers remains the same.
The ellipse reduces to a single line.
Note that as soon as the two circles are separated, the locus of the
center of the tangent circle becomes hyperbolic in shape.
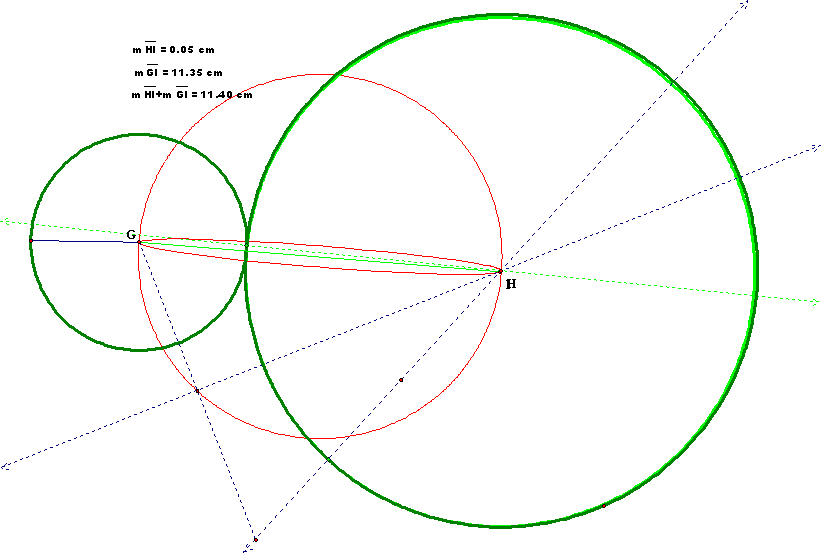
Problem 7.6: Discuss the locus of the centers of the
constructed tangent circles when the two given circles intersect.
Per the inclusion of the locus of the centers of the tangent circle in
#5 above, and through the measurement of the segments, the segment totals
remain the same, as the center moves around each of the centers of the 2 given
circles. This would describe again an
ellipse with foci at the centers of the two given circles.
Problem 7.7: Investigate, discuss and state conjectures
about the locus of the centers of the set of constructed tangent circles in # 5
and #6.
Problem 7.8: Discuss the construction of the circles
tangent to two given circles when two circular regions are disjoint.
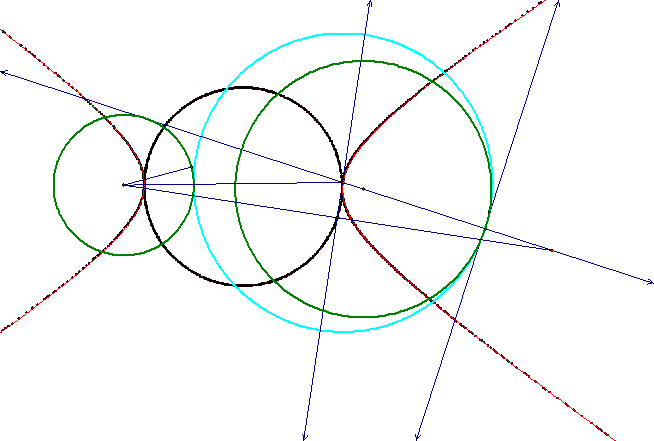
The above sketch shows the construction of two circles with a circle
tangent to both, when the original circles are disjoint. The locus of the center of the tangent circle
creates a hyperbolic trace about each of the centers of the original
circles.