Assignment # 8
Fall 2002 Semester
GSP - Alttitudes and Orthrocenters
Altitudes
and Orthocenters
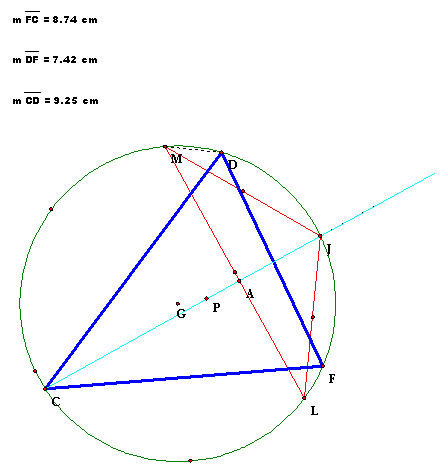
Problem 8.10:
Examine the triangle formed by the points where the extended altitudes
meet the circumcircle.

How is this triangle
(triangle CDF) related to the Orthic triangle? (triangle ABE):
It appears to be a
similar triangle, with each side twice the length of itís corresponding side
of the Orthic triangle.
i.e. AB/CD = BE/DF =
EA/FC = 1/2
Proof:
1.
Construct the nine point circle for triangle MJL.
Note that the vertices for triangle ABE fall on the nine point circle (by
definition).

3.
This means that the line segments between the orthocenter and the
circumcircle are bisected by the nine point circle.
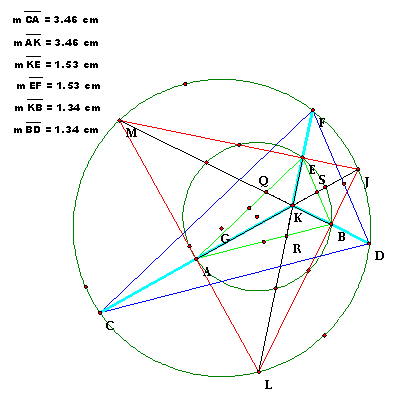
4.
Length of AK/CK = BK/DK = EK/FK = 1/2
5.
Therefore triangle BKE is similar to triangle DKF, with

6.
Therefore BE/DF = 1/2
7.
Similarly, AB/CD = AE/CF = 1/2
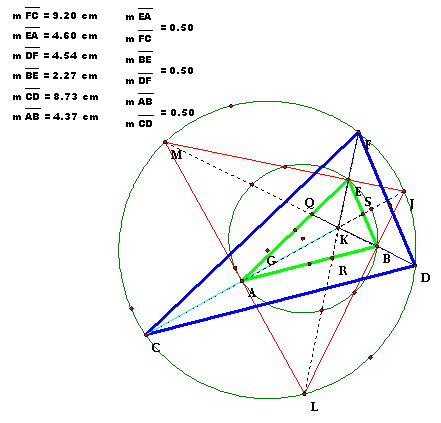
8.
Since all the segments between triangle ABE and triangle CDF are all
ratio Ĺ to each other, then the two triangles are similar.
Since all the lengths are related by a factor of 1 to 2, the triangle
areas are related by the square of the linear relationship, i.e. the CDF is 4
times the are of triangle ABE.
Will the
relationship hold, if the the original triangle is obtuse?
The relationship
doesnít hold as we make the original triangle obtuse.
We lose the relationship as the perpendicular falls exterior to the
triangle.