Assignment # 9
Fall 2002 Semester
GSP - Pedal Triangles
Pedal Triangles
Observation 9.11 Envelope of
the Simson Line
1.
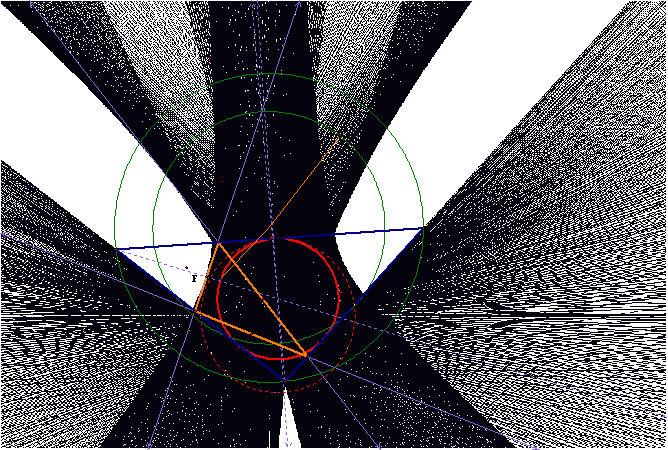
Traces of Pedal point around the circumcircle,
circle with radius greater than
the circumcircle and incircle.
2.
Within each of the circle traces, include changes to the original
triangle for equilateral triangle, isosceles triangle and obtuse angle triangle.
Conclusions:
The envelope of the Simson line of the triangle ABC is the deltoid area (tricuspoid)
displayed in the attached sketches. The
area of the deltoid is one half the area of the circumcircle.
Also, each side of the
triangle is tangent to the deltoid at a point whose distance from the midpoint
of the side equals the chord of the
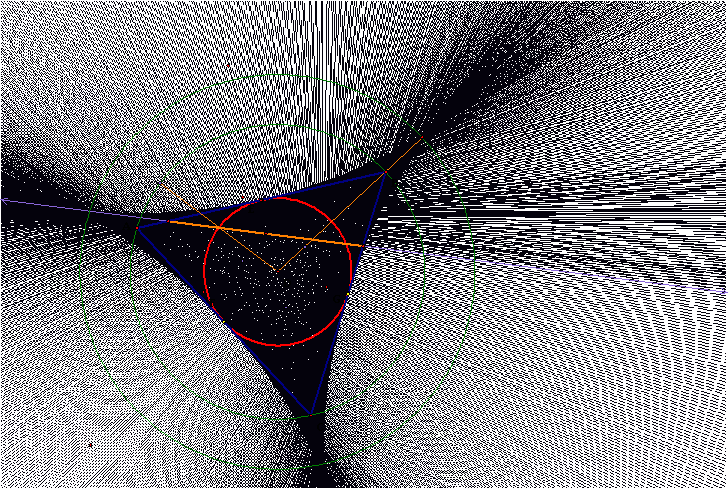
Equilateral Triangle: The
sketch below shows the deltoid created by the traces of the line traced by the
Simson line as the Petal point is rotated around the circumcircle.
Essentially, the tangent point of the deltoid area is at the midpoint of
each side.

When the triangle consists of 2 acute and one obtuse angle, then the
traced area now lines up with the nine-point circle, as shown….
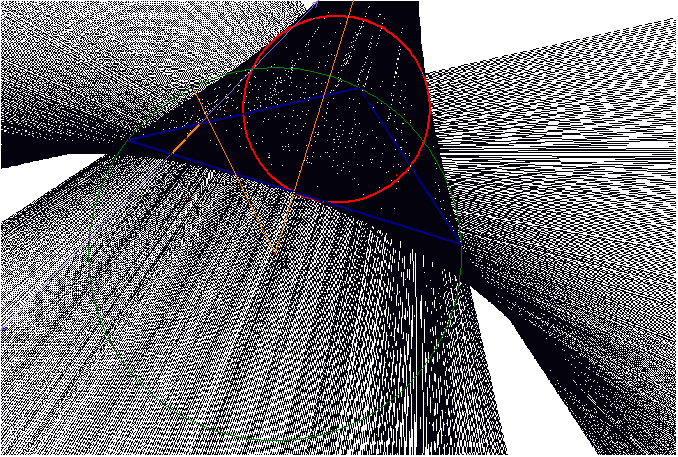
Note that for an isosceles triangle, we’ll end up with the tangent
being at the midpoint on one of the sides and the other two congruent sides will
have the same relative tangential point to the midpoint of the side.
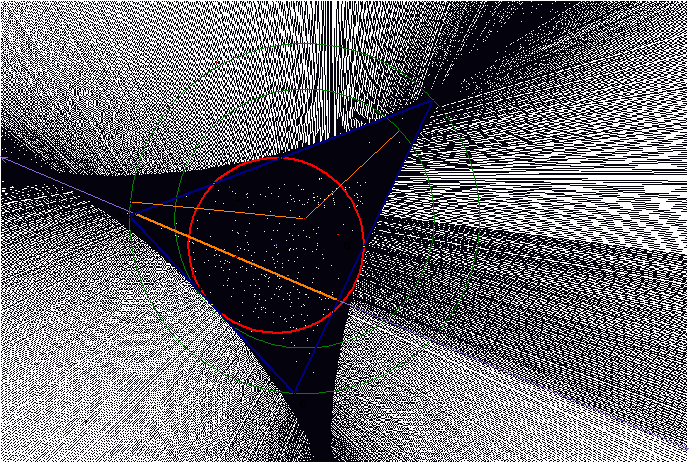
When we trace the Simson line with the Petal point traveling on a circle
slightly larger than the circumcircle, then the pattern resembles the pattern we
showed with the Petal point traveling along the circumcircle.
In this case, the tangent points with the sides disappear and the shape
is no longer the tricuspoid we saw with the circumcircle.
The sketch below is when there were 3 acute angles in the original
triangle.
The diagram below shows the
sketch of when the triangle is equilateral.
The shape is the same as in the 3 acute angles.
There is less area of this trace within the triangle as for the first
case. Also note that the vertices
are the limits for the trace area.
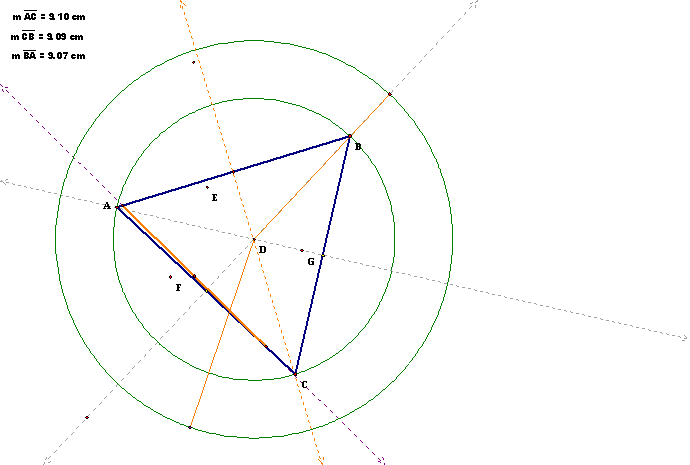

For the isosceles triangle, more of the triangle area is covered by the
trace. The congruent sides
resemble each other in this case.
Incircle traces for the cases of isosceles shown in the sketch below. This more resembles the case of the trace about the circumcircle. More of the circumcircle area is covered by this trace than in the circumcircle trace above.
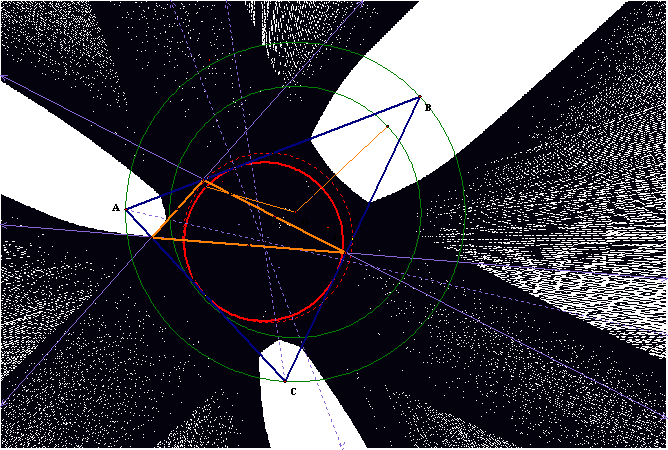
The next sketch shows the same type of trace for an equilateral
triangle. Note how the blank trace
area is more consistent between the vertices, as would be expected.
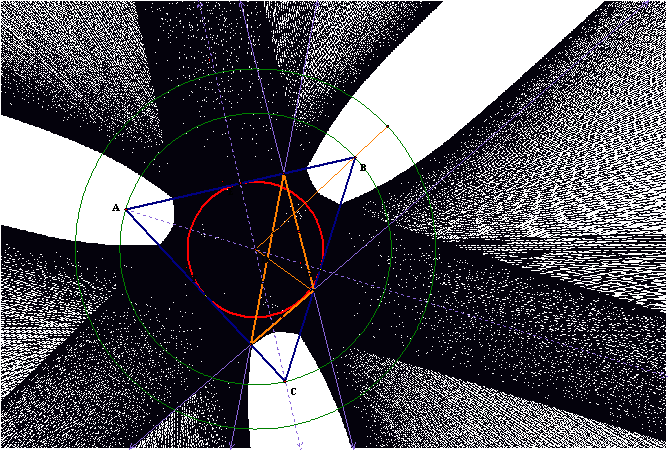
The last triangle is a general triangle with an obtuse angle.
As would be expected, the area of no traces is greater where the angles
are more acute. The no trace area is
much less as the angle becomes more obtuse.