Making Sense of the
Directrix and
Focus of a Parabola!
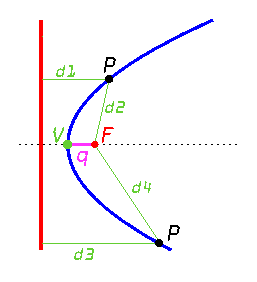How many times have
you been given the definitions of terms like the locus, the directrix,
and the focus of a parabola? Did you memorize the definitions
so that you might regurgitate them on a test? Did you ever fully
understand what they were? If you think that you understood it
when you were 17, do you still understand?
The definitions seem
quite simple:
parabola: The locus of points
in the plane whose distances from a fixed point, called the focus,
and a fixed line, called the directrix, are equal.
So, from this definition,
you now know exactly what a parabola is.
Oh, wait. What's a
locus you ask? It is merely a set of points satisfying a
condition. From the definition above, it is the parabola.
I want you to be able
to "see" this so I am going to call on my old friend,
Geometer's Sketchpad. First, I want to show the x-axis and the
y-axis, so I highlight "show grid." This is not necessary,
but maybe more helpful at placing your directrix and
focus. Place an arbitrary point on your graph, the focus,
and an arbitrary line, the directrix. I chose my directrix to
be the x-axis and my focus is the point (3,2). Place a "movable"
point on the directrix, construct a segment from that point
to the focus, and construct the midpoint of that
new segment. This ensures that this point on the directrix is equidistant from the focus. Now,
when we move the point along the directrix, the
midpoint of this segment will always keep the focus equidistant
from that particular point on the directrix; however,
the distance from a point to a line is found by drawing a perpendicular
line through the point to the line. Now, it is necessary to draw
this perpendicular line through our movable point to the directrix (which is my x-axis). The point where they intersect,
is that magical point where the focus and directrix are equidistant. When we plot a set
of these points, we have a beautiful parabola!
To see this as an animation,
click
here.
Now, for those of you
that have had Calculus, you may notice a special relationship
above in the blue line and the parabola. The blue line is the
tangent line to the parabola. This allows us to
make even more connections involving the first derivative of a
function (we are specifically looking at a quadratic function).
To see this as an animation,
click
here.
There are fun ways
to develop other conic sections like the ellipse and the hyperbola
using Geometer's Sketchpad.
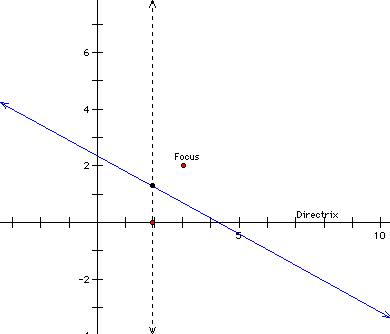
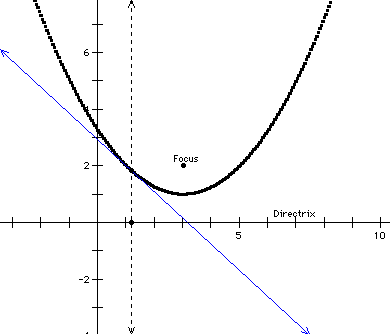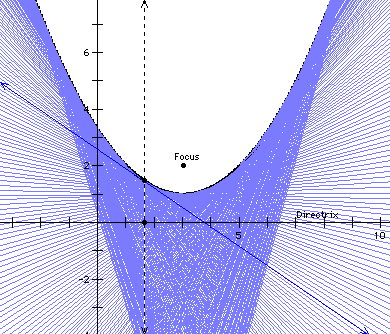To see this as an animation,
click here.
To see this as an animation,
click
here.
Return