The effects of changing a, b, & c in the function
y = a sin(bx + c)

First, I am going to assume that everyone knows the following trigonometric ratios:
sin 0 = 0
sin p/2 = 1
sin p = 0
sin 3p/2 = -1
sin 2p = 0
One must also know that the sin curve is a periodic function because it produces a pattern that repeats over and over the length of the period, ie., if the period is 2, the graph will repeat every 2 units.
Investigation of a
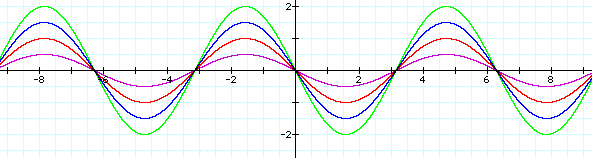
I want to know what happens when you change the value of a, so I am going to let b = 1 and c = 0. I want to see large values of a, small values of a, fractions, and negatives. First, I want to look at positive values of a. Then, on a separate graph, I want to look at negative values of a.
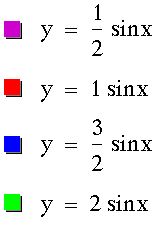
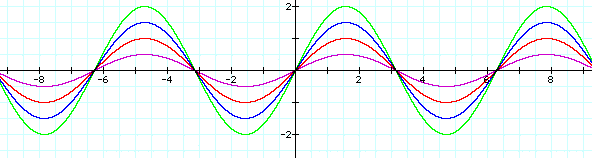
There seems to be a connection in the graphs so I am going to plot a = 2 and a = -2 on the same graph.
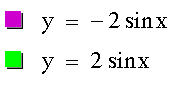
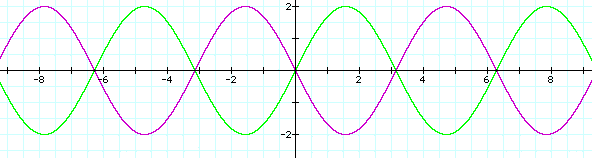
Click here to see my investigation as a movie.
From studying the changes in a, all of the graphs intersect the x-axis at the same values (0, p, -p, etc.). It also appears as if the graph moves between +a and -a on the y-axis. When a is positive, all graphs move upward to the right of the y-axis and when a is negative, all graphs move downward to the right of the y-axis. When plotting a and -a on the same graph, we can see that they are mirror images about the x-axis moving between a and -a.
Actually, a signifies the amplitude of the graph meaning that its absolute value is the maximum distance away from the x-axis. This is clearly shown as we look at the original graph of y = sinx. The amplitude in this case is 1 and our graph moves between -1 and 1. In the graph of y = 2sinx, we can see that the curve moves between -2 and 2 because the amplitude is 2. In the same graph, we see y = -2sinx, which also has an amplitude of 2 and moves between -2 and 2. Looking at the original trigonometric ratios that I assumed everyone knew, you can see that -2 * y-values yields a y-table of: 0, -2, 0, 2, 0. This explains why the graphs with a -a appear to go down to the right of the y-axis and why the graphs with a a go up to the right of the y-axis.
Investigation of b
In my investigation of b, I will now let a =1 and c = 0. Like before, I am going to try large values of b, small values, fractions, and negatives. First, I want to look at postive values of b.
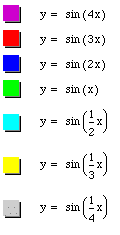
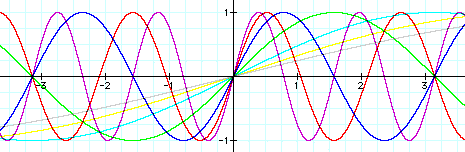
From these graphs, we can see that they all pass through the origin. We can also see that the period becomes shorter or longer depending on the b value. The smaller the number, the longer the period and the larger the number, the shorter the period.
Next, I wanted to look at negative values of b. I had a very similar graph to the one above, so I decided to look at a particular case of b = 2 and -2.
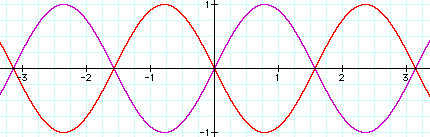
From this, we can see the negative angle identity for sin.
sin(-x) = -sinx
Click here to see my investigation as a movie.
Investigation of c
Lastly, I want to investigate what happens when the value of c changes as I let a = b = 1.
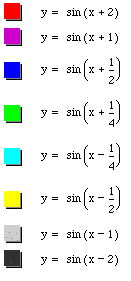
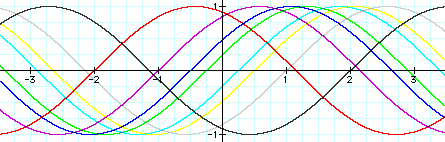
The changing of c causes the phase shifts - the graphs are all identical but are shifted horizontally.
Click here to see my investigation as a movie.