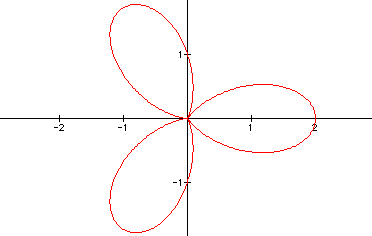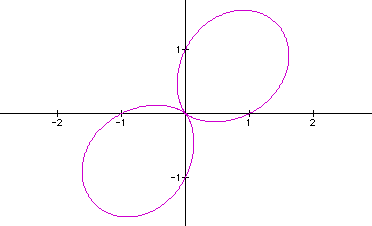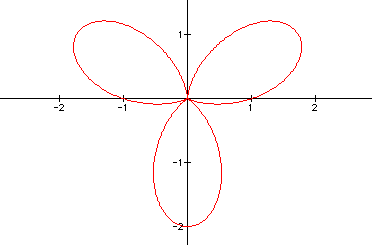Fun with Basic Polar
Equations
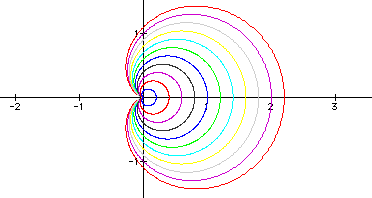
r = a + b*cos(kq)
If a and b
are equal and k is an integer, what do these graphs
look like? First, let's look at a
= b = +/-0.1, a = b = +/-0.2,... a = b =
+/-1, a = b = +/-1.1.
 Let's separate these
two graphs into +a = +b and -a
= -b.
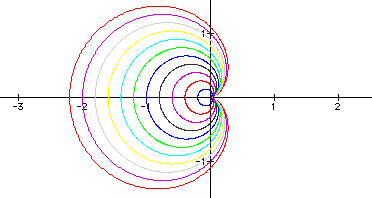
Let's separate these
two graphs into +a = +b and -a
= -b.
 If a and b
are negative, it just flips the graph of a and b
being positive. It also looks like the graph crosses the y-axis
at +a and -a and crosses the x-axis at 2*a
and 0 when a = b. This is called the "n-leaf rose"
from Dr. Wilson's home page. Now, is the a really necessary
in the equation? What happens when the a is removed?
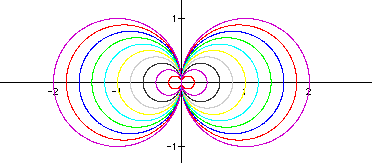
This time, I let b = +/-
0.2, 0.4, ..., 1.8, 2.0.
r = b*cos(kq)
If a and b
are negative, it just flips the graph of a and b
being positive. It also looks like the graph crosses the y-axis
at +a and -a and crosses the x-axis at 2*a
and 0 when a = b. This is called the "n-leaf rose"
from Dr. Wilson's home page. Now, is the a really necessary
in the equation? What happens when the a is removed?
This time, I let b = +/-
0.2, 0.4, ..., 1.8, 2.0.
r = b*cos(kq)
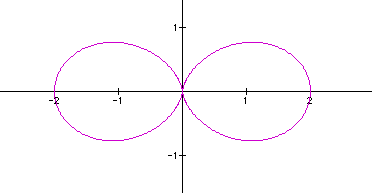
 It is now very apparent
that the graph crosses the x-axis at 0 and b. The graph
only crosses the y-axis at 0 so the a in the previous
equation did tell us where the graph would cross the y-axis (-a
and a).
For all of the graphs
thus far, k = 1. What if k = 2 or -2
or 1/2? I am going to look at the original equation first where
a = b = 1.
r = a + b*cos(kq)
k = 2
It is now very apparent
that the graph crosses the x-axis at 0 and b. The graph
only crosses the y-axis at 0 so the a in the previous
equation did tell us where the graph would cross the y-axis (-a
and a).
For all of the graphs
thus far, k = 1. What if k = 2 or -2
or 1/2? I am going to look at the original equation first where
a = b = 1.
r = a + b*cos(kq)
k = 2
 k = -2 is really boring -- it looks just like the graph
of k = 2. Let's assume that -k looks the
same as +k. This is not hard to believe since
cos q = cos (-q)!
k = 3
k = -2 is really boring -- it looks just like the graph
of k = 2. Let's assume that -k looks the
same as +k. This is not hard to believe since
cos q = cos (-q)!
k = 3
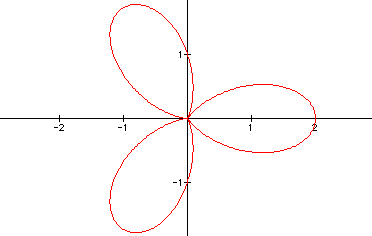 k = 4
k = 4
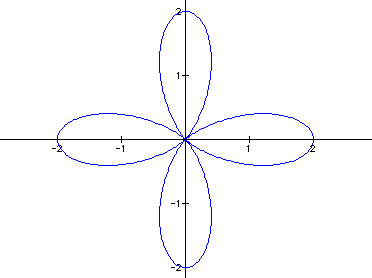 It seems that our "flower"
will have as many petals as there are k's. So, if
k = 10, will we have 10 petals?
It seems that our "flower"
will have as many petals as there are k's. So, if
k = 10, will we have 10 petals?
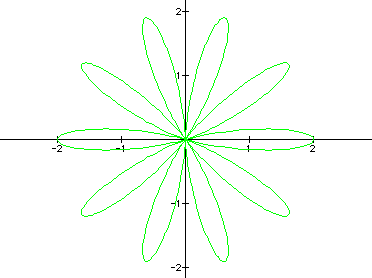 YES! What if k
is not an integer? Let's look at k = 1.0, 1.1,
1.2, ..., 1.8, 1.9, 2.0.
YES! What if k
is not an integer? Let's look at k = 1.0, 1.1,
1.2, ..., 1.8, 1.9, 2.0.
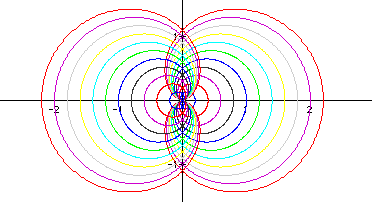
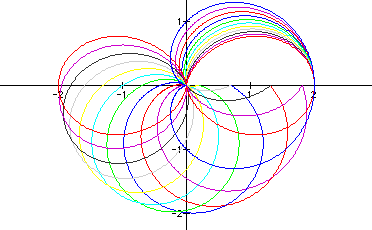 Wow! That is one crazy
looking graph!
Now, what happens when
the a is removed for different integer values of k
where b = 1?
r = b*cos(kq)
k = 2
Wow! That is one crazy
looking graph!
Now, what happens when
the a is removed for different integer values of k
where b = 1?
r = b*cos(kq)
k = 2
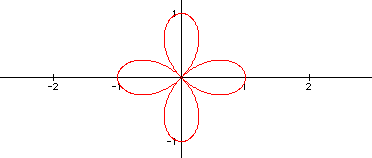 k = 3
k = 3
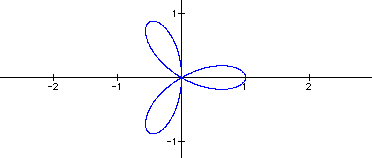 k = 4
k = 4
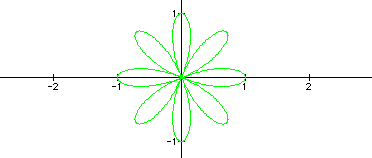 k = 5
k = 5
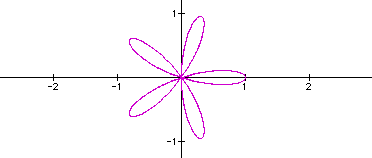 I think that if k is
odd, there would be k petals in the flower and if k
was even, there would be 2k petals in the flower. Just to make
sure, let's look at k =
10. If my conjecture is
correct, there will be 20 petals on the flower.
I think that if k is
odd, there would be k petals in the flower and if k
was even, there would be 2k petals in the flower. Just to make
sure, let's look at k =
10. If my conjecture is
correct, there will be 20 petals on the flower.
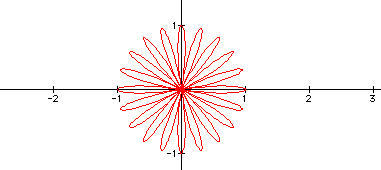 Yea! There are 20 petals!
What would happen to my graphs if b was changed
to 2?
Yea! There are 20 petals!
What would happen to my graphs if b was changed
to 2?
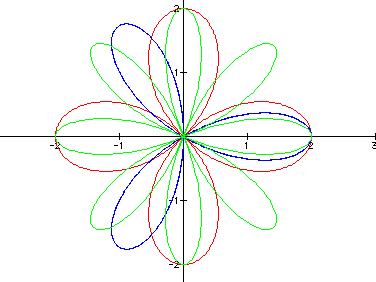 All that changed was
that the length of the petals changed to 2. Therefore, the length
of the petals equals b.
What if the cos is
replaced with sin?
r = a + b*sin(kq)
If a and b
are equal and k is an integer, what do these graphs
look like? First, let's look at a
= b = 0.1, 0.2,...,
1, 1.1.
All that changed was
that the length of the petals changed to 2. Therefore, the length
of the petals equals b.
What if the cos is
replaced with sin?
r = a + b*sin(kq)
If a and b
are equal and k is an integer, what do these graphs
look like? First, let's look at a
= b = 0.1, 0.2,...,
1, 1.1.
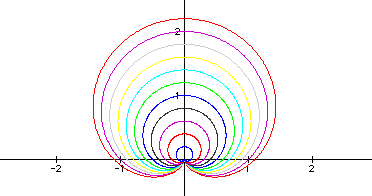 I think that it is
safe to say that if a = b = -value, the graph would be reflected
about the x-axis like it was reflected about the y-axis for cos.
Will the graph rotate 90 degrees for other equations of sin? What
if a = b = 1 and
k = 2?
I think that it is
safe to say that if a = b = -value, the graph would be reflected
about the x-axis like it was reflected about the y-axis for cos.
Will the graph rotate 90 degrees for other equations of sin? What
if a = b = 1 and
k = 2?
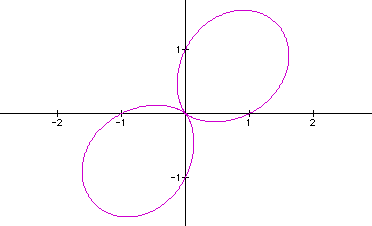 It is definitely not
a 90 degree rotation, but a rotation none the less. What if a = b = 1 and k = 3?
It is definitely not
a 90 degree rotation, but a rotation none the less. What if a = b = 1 and k = 3?
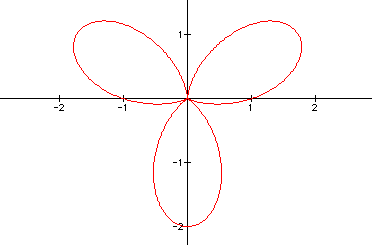 What if a = b = 1 and k = 4?
What if a = b = 1 and k = 4?
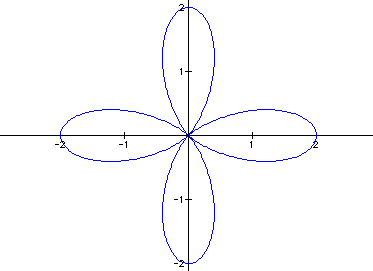 What if a = b = 1 and k = 10?
What if a = b = 1 and k = 10?
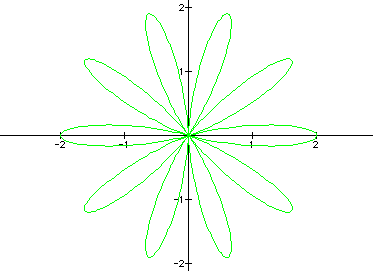 Changing the cosine
to sine in the equation is not that exciting in my opinion. It
only rotates the graph about 45 degrees (?).
Changing the cosine
to sine in the equation is not that exciting in my opinion. It
only rotates the graph about 45 degrees (?).
Return