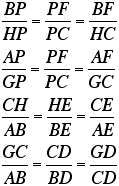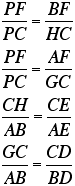Final Assignment!!

 

The final assignment for EMAT 6680 involves a triangle and an arbitrary point inside the triangle. We are going to explore some ratios that come out of this sketch and hopefully prove why the ratios are what they are. The following GSP sketch was made by constructing a triangle, that arbitrary point P, and the lines through the point and the vertices.

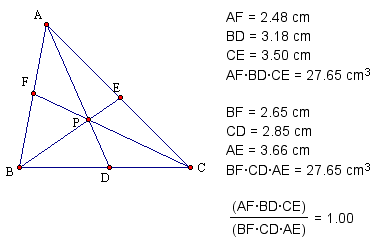What do you know? The ratio is 1!

Click here to drag point P in the GSP sketch to see if it is always one.

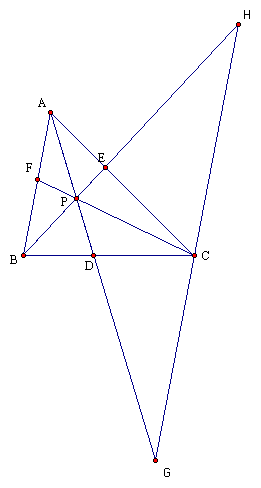I have constructed a line through vertex C that is parallel to segment AB. Then, I extended the line segments through the other two vertices until they intersected my new line GH. We now have similar triangles in BPF and HPC, APF and GPC, CHE and ABE, and GCD and ABD using the Angle-Angle Theorem for similar triangles because the vertical angles are congruent and the alternate interior angles congruent. Since corresponding sides of similar triangles are in proportion, we have the following proportions:

 

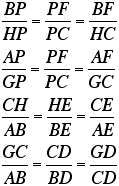Now, you may ask what in the world are all of these proportions going to do for us? We don't need all of them, just these:

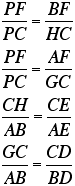Using simple laws of proportions, we see that

.

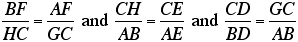From the first of these ratios, we have a new ratio:

.

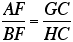Now, using some fancy footwork and substitution of equivalent ratios, we end up with the following proportion:

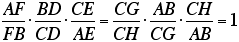Therefore, the ratio will always be one!

I did get some help with this proof. Click here to view the web page and proof.

 

Next, I want to look at this ratio if point P is outside the triangle. Does the generalization hold?

 

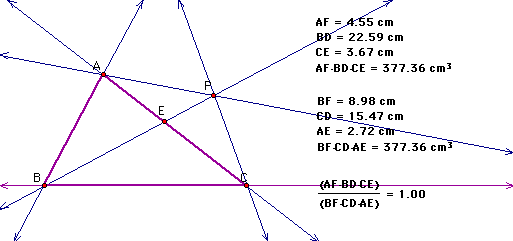Click here to drag point P to see if the ratio will always be one.

 

For my last trick, I am going to show that the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4.

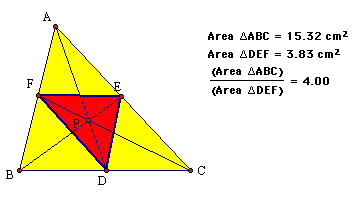Apparently, the ratio of the areas is equal to 4 if point P is the centroid of the circle. If P is not the centroid, the ratio is greater than 4. Click here to drag point P in a GSP sketch to see that this is always true.

 

 

 

---

Return

---