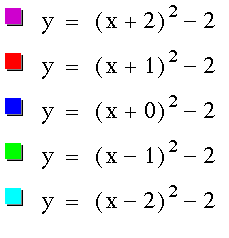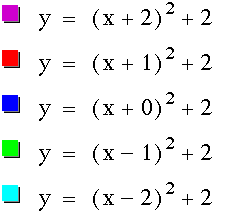Varying d
in the Equation
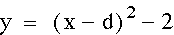 In this investigation,
I would like to see what happens to the graph of the given function
by changing the value of d.
First, I will graph
the function with d = -2, -1, 0, 1, 2.
In this investigation,
I would like to see what happens to the graph of the given function
by changing the value of d.
First, I will graph
the function with d = -2, -1, 0, 1, 2.
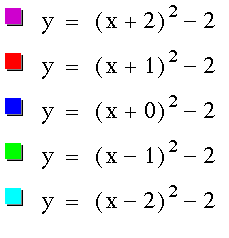
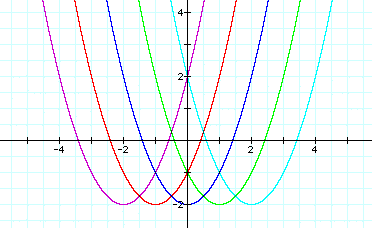 All of the graphs have
a vertex with a y-value of -2. Does this come from the - 2 at
the end of each equation? What happens if it is a + 2 instead?
All of the graphs have
a vertex with a y-value of -2. Does this come from the - 2 at
the end of each equation? What happens if it is a + 2 instead?
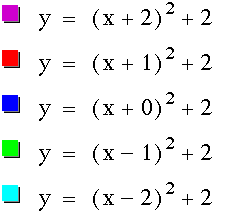
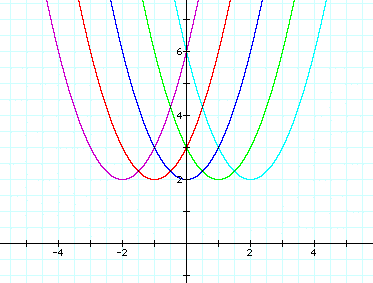 This leads me to believe
that a quadratic equation written in this form will have a vertex
with a y-value of the number added to the end.
click here to see this investigation as a movie.
(I have let d=0 and am calling the number added
to the end k. I let k run from
-5 to 5.)
Back to the question
at hand -- what happens when the value of d is changed?
If d
=1, we have:
This leads me to believe
that a quadratic equation written in this form will have a vertex
with a y-value of the number added to the end.
click here to see this investigation as a movie.
(I have let d=0 and am calling the number added
to the end k. I let k run from
-5 to 5.)
Back to the question
at hand -- what happens when the value of d is changed?
If d
=1, we have:
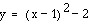
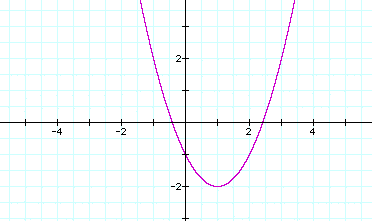 This graph has a vertex
(1,-2).
If d
= 2, we have:
This graph has a vertex
(1,-2).
If d
= 2, we have:
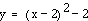
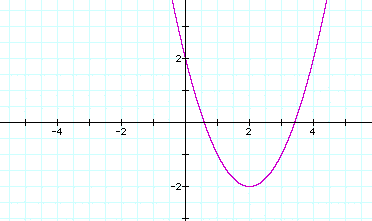 This graph has a vertex
(2,-2).
If d
= 3, we have:
This graph has a vertex
(2,-2).
If d
= 3, we have:
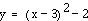
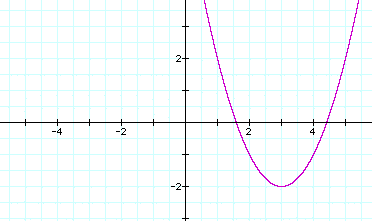 This graph has a vertex
(3,-2).
If d
= -1, we have:
This graph has a vertex
(3,-2).
If d
= -1, we have:
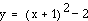
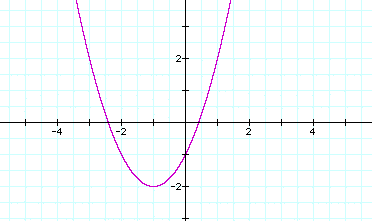 This graph has a vertex
(-1,-2).
If d
= -2, we have:
This graph has a vertex
(-1,-2).
If d
= -2, we have:
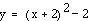
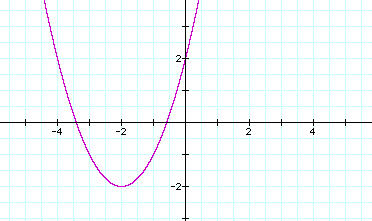 This graph has a vertex
(-2,-2).
I think that it becomes
very obvious that whenever you have a quadratic equation in this
form, the vertex will lie at: (d,k).
This graph has a vertex
(-2,-2).
I think that it becomes
very obvious that whenever you have a quadratic equation in this
form, the vertex will lie at: (d,k).
Return