An Investigation of
Triangle Centers
 This page is designed
so that high school students can explore triangles and their centers
using Geometer's Sketchpad. They will investigate centroids, orthocenters,
circumcenters, and incenters. Students may draw conclusions based
on the constructions -- some of which will be theorems that are
to be proven in class.
Centroid
The centroid of a triangle
involves constructing all of the medians on a triangle. Let's
start with an acute triangle and construct the medians. Do you
notice anything special? What would happen if we started with
an obtuse triangle? What about a right triangle? [Instead, of
starting over with an obtuse triangle, choose a vertex of the
acute triangle and drag it until it makes the triangle obtuse.
Do the same for the right triangle.]
This page is designed
so that high school students can explore triangles and their centers
using Geometer's Sketchpad. They will investigate centroids, orthocenters,
circumcenters, and incenters. Students may draw conclusions based
on the constructions -- some of which will be theorems that are
to be proven in class.
Centroid
The centroid of a triangle
involves constructing all of the medians on a triangle. Let's
start with an acute triangle and construct the medians. Do you
notice anything special? What would happen if we started with
an obtuse triangle? What about a right triangle? [Instead, of
starting over with an obtuse triangle, choose a vertex of the
acute triangle and drag it until it makes the triangle obtuse.
Do the same for the right triangle.]
 Construct any triangle and its centroid.
You may want to hide the segments that are the medians. Now, construct
segments from each vertex and midpoint to the centroid -- it should
look exactly the same as before you hid the medians. Using the
measure segment function in Geometer's Sketchpad, measure each
of the segments. Do you see any relationship in the distance from
the vertex to the centroid to the distance from the centroid to
the midpoint? Make a hypothesis and try it out on several different
triangles.
Construct any triangle and its centroid.
You may want to hide the segments that are the medians. Now, construct
segments from each vertex and midpoint to the centroid -- it should
look exactly the same as before you hid the medians. Using the
measure segment function in Geometer's Sketchpad, measure each
of the segments. Do you see any relationship in the distance from
the vertex to the centroid to the distance from the centroid to
the midpoint? Make a hypothesis and try it out on several different
triangles.
 The centroid, G, of a triangle is the common intersection
of the three medians.
The medians of a triangle
intersect in a point that is 2/3 of the distance from each vertex to
the midpoint of the opposite side.
The centroid is also called the center
of gravity. If you were to cut out a triangle out of cardboard
and construct its centroid, it would be perfectly balanced at
this point.
Orthocenter
The orthocenter of
a triangle involves constructing the altitudes of the triangle.
Construct an acute triangle and its altitudes (altitudes are lines
that are perpendicular to a side of the triangle and go through
the opposite vertex). Do you notice anything special about the
intersection of the altitudes? What would happen if we had started
with an obtuse triangle or a right triangle? Make a hypothesis
about each type of triangle and its orthocenter and they try it
out for several triangles.
The centroid, G, of a triangle is the common intersection
of the three medians.
The medians of a triangle
intersect in a point that is 2/3 of the distance from each vertex to
the midpoint of the opposite side.
The centroid is also called the center
of gravity. If you were to cut out a triangle out of cardboard
and construct its centroid, it would be perfectly balanced at
this point.
Orthocenter
The orthocenter of
a triangle involves constructing the altitudes of the triangle.
Construct an acute triangle and its altitudes (altitudes are lines
that are perpendicular to a side of the triangle and go through
the opposite vertex). Do you notice anything special about the
intersection of the altitudes? What would happen if we had started
with an obtuse triangle or a right triangle? Make a hypothesis
about each type of triangle and its orthocenter and they try it
out for several triangles.


 The orthocenter, H, of a triangle is the common intersection
of the three lines containing the altitudes.
If the triangle is
acute, the orthocenter will lie inside the triangle. If the triangle
is obtuse, the orthocenter will lie outside the triangle. If the
triangle is right, the orthocenter will lie on the vertex that
corresponds with the right angle.
Circumcenter
The circumcenter of
a triangle involves constructing the perpendicular bisectors of
a triangle. Again, we will start with an acute triangle and construct
the perpendicular bisector of each side (construct the midpoint
of each side and then choose the side and the midpoint to construct
the perpendicular line). By now, you should realize that the lines
are to intersect at the same point. Do you notice anything special
about the intersection of the perpendicular bisectors? Using this
intersection and a vertex on the triangle, construct a circle.
What do you notice now? Does changing the original triangle to
an obtuse or a right change anything?
The orthocenter, H, of a triangle is the common intersection
of the three lines containing the altitudes.
If the triangle is
acute, the orthocenter will lie inside the triangle. If the triangle
is obtuse, the orthocenter will lie outside the triangle. If the
triangle is right, the orthocenter will lie on the vertex that
corresponds with the right angle.
Circumcenter
The circumcenter of
a triangle involves constructing the perpendicular bisectors of
a triangle. Again, we will start with an acute triangle and construct
the perpendicular bisector of each side (construct the midpoint
of each side and then choose the side and the midpoint to construct
the perpendicular line). By now, you should realize that the lines
are to intersect at the same point. Do you notice anything special
about the intersection of the perpendicular bisectors? Using this
intersection and a vertex on the triangle, construct a circle.
What do you notice now? Does changing the original triangle to
an obtuse or a right change anything?
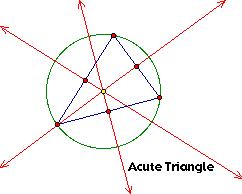

 Construct any triangle
and its circumcenter. You may hide the perpendicular bisectors
needed to find the circumcenter. Now, construct the segments from
each vertex to the circumcenter. Using the measure segment function
in Geometer's Sketchpad, measure each segment. Do you notice any
special relationship? Make a hypothesis and test it on several
different triangles. Does it work for acute triangles? obtuse
triangles? right triangles?
Construct any triangle
and its circumcenter. You may hide the perpendicular bisectors
needed to find the circumcenter. Now, construct the segments from
each vertex to the circumcenter. Using the measure segment function
in Geometer's Sketchpad, measure each segment. Do you notice any
special relationship? Make a hypothesis and test it on several
different triangles. Does it work for acute triangles? obtuse
triangles? right triangles?
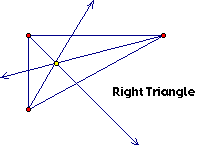
 Let's expand on this
in the case of the right triangle. Construct the circumcenter
on a right triangle. Construct a segment from each vertex of the
hypotenuse to the circumcenter. What relationship do you notice
about the circumcenter and the hypotenuse? Make a hypothesis and
test it for several right triangles.
Let's expand on this
in the case of the right triangle. Construct the circumcenter
on a right triangle. Construct a segment from each vertex of the
hypotenuse to the circumcenter. What relationship do you notice
about the circumcenter and the hypotenuse? Make a hypothesis and
test it for several right triangles.
 The circumcenter,
C, of a triangle is the point in the plane equidistant from the
three vertices of the triangle.
The circumcenter
will always coincide with the midpoint of the hypotenuse of a
right triangle.
Incenter
The incenter of a triangle
involves constructing the angle bisectors. We will start by constructing
an acute triangle with its angle bisectors. Do you notice anything
special about the intersection of the angle bisectors? What if
we had started with an obtuse triangle or a right triangle?
The circumcenter,
C, of a triangle is the point in the plane equidistant from the
three vertices of the triangle.
The circumcenter
will always coincide with the midpoint of the hypotenuse of a
right triangle.
Incenter
The incenter of a triangle
involves constructing the angle bisectors. We will start by constructing
an acute triangle with its angle bisectors. Do you notice anything
special about the intersection of the angle bisectors? What if
we had started with an obtuse triangle or a right triangle?


 Now, hide the angle
bisectors. Construct a perpendicular segment from the incenter
to any side. Using the incenter as the center and the point of
intersection of the perpendicular line to the side as another
point, make a circle. What do you notice about the circle? Make
a hypothesis and test it for several triangles.
Now, hide the angle
bisectors. Construct a perpendicular segment from the incenter
to any side. Using the incenter as the center and the point of
intersection of the perpendicular line to the side as another
point, make a circle. What do you notice about the circle? Make
a hypothesis and test it for several triangles.
 The incenter, I,
of a triangle is the point on the interior of the triangle that
is equidistant from the three sides.
Euler Line
Now, let's see if there
are any relationships between these centers of a triangle. Construct
any triangle with the centroid, orthocenter, circumcenter, and
incenter labeling them G, H, C, and I, respectively. Construct
a segment between each pair of points. Your construction may be
too cluttered, so you may delete the incenter for now - we will
return to it later. Do you notice a special relationship in these
points?
The incenter, I,
of a triangle is the point on the interior of the triangle that
is equidistant from the three sides.
Euler Line
Now, let's see if there
are any relationships between these centers of a triangle. Construct
any triangle with the centroid, orthocenter, circumcenter, and
incenter labeling them G, H, C, and I, respectively. Construct
a segment between each pair of points. Your construction may be
too cluttered, so you may delete the incenter for now - we will
return to it later. Do you notice a special relationship in these
points?


 The centroid, circumcenter,
and orthocenter always lie on a straight line -- the Euler Line.
Do you notice any special
relationship between the distances between the points?
The centroid, circumcenter,
and orthocenter always lie on a straight line -- the Euler Line.
Do you notice any special
relationship between the distances between the points?
 The distance from the
orthocenter to the centroid is always twice as long as the distance
from the centroid to the circumcenter.
Now, add the incenter
to the construction. Do you notice anything special about the
incenter with its relation to the Euler Line?
The distance from the
orthocenter to the centroid is always twice as long as the distance
from the centroid to the circumcenter.
Now, add the incenter
to the construction. Do you notice anything special about the
incenter with its relation to the Euler Line?
 The incenter lies on
the Euler Line if the triangle is isosceles.
What happens to the
points if the triangle is equilateral?
The incenter lies on
the Euler Line if the triangle is isosceles.
What happens to the
points if the triangle is equilateral?
 If the triangle is
equilateral, the points are concurrent.
If the triangle is
equilateral, the points are concurrent.
Return





















