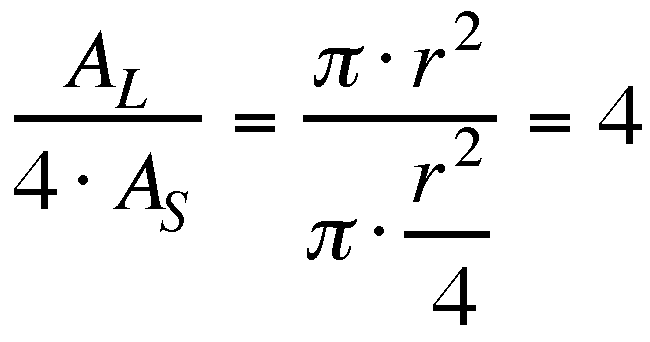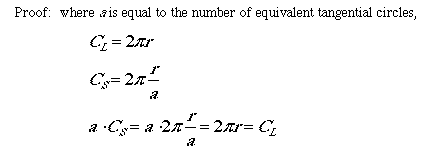Tangent Along the Diameter
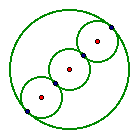
 Along the diameter
of a circle you can construct circles with equal radii that are
tangent to each other. The outermost circles in the string of
circles will be tangent to the large circle. (Tangent means that
the circles touch each other but do not cross over each other,
nor do they leave any gaps.)
How does the combined
area of all of the shaded circles relate to the area of the entire
circle?
This problem was
found on the Intermath
site at:
http://www.intermath-uga.gatech.edu/topics/geometry/circles/r03.htm
Along the diameter
of a circle you can construct circles with equal radii that are
tangent to each other. The outermost circles in the string of
circles will be tangent to the large circle. (Tangent means that
the circles touch each other but do not cross over each other,
nor do they leave any gaps.)
How does the combined
area of all of the shaded circles relate to the area of the entire
circle?
This problem was
found on the Intermath
site at:
http://www.intermath-uga.gatech.edu/topics/geometry/circles/r03.htm
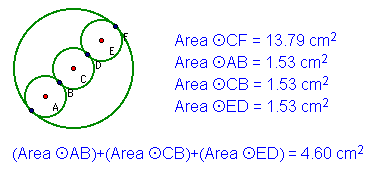 Click
here to view the GSP file to change
the size of the circles (move point B).
The most obvious operation to apply
here to find the relationship between the sum of the areas of
the smaller tangent circles to the area of the larger circle,
is to divide the area of the larger by the sum of the smaller
areas. In changing the size of the circles, it was very consistently
approximately 3. It is probably not exactly 3 every time due to
rounding of the value of pi. This should be obvious from the given
picture since each smaller circle has a diameter equal to one-third
of the diameter of the larger circle. In the following "proof,"
A sub L represents the area of the large circle and A
sub S represents the area of the small circles.
Click
here to view the GSP file to change
the size of the circles (move point B).
The most obvious operation to apply
here to find the relationship between the sum of the areas of
the smaller tangent circles to the area of the larger circle,
is to divide the area of the larger by the sum of the smaller
areas. In changing the size of the circles, it was very consistently
approximately 3. It is probably not exactly 3 every time due to
rounding of the value of pi. This should be obvious from the given
picture since each smaller circle has a diameter equal to one-third
of the diameter of the larger circle. In the following "proof,"
A sub L represents the area of the large circle and A
sub S represents the area of the small circles.
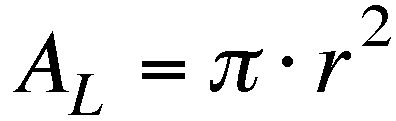
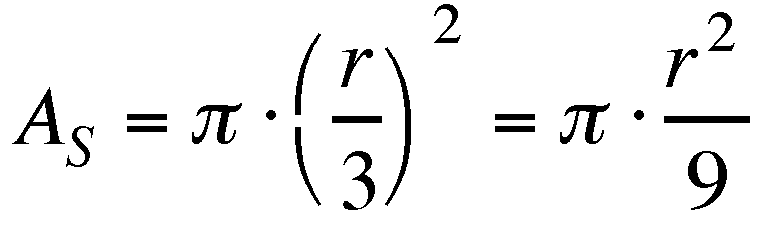
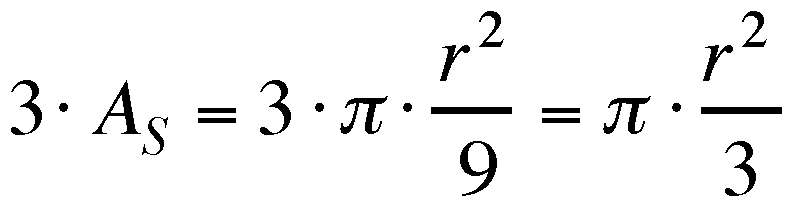
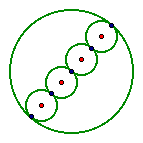
 In making the connection above, it
now seems very obvious that the sum of the four small tangent
circles along the diameter of the large circle should be 1/4 of
the area of the large circle. Again, we have small circles that
have a diameter equal to 1/4 of the diameter of the large circle.
In making the connection above, it
now seems very obvious that the sum of the four small tangent
circles along the diameter of the large circle should be 1/4 of
the area of the large circle. Again, we have small circles that
have a diameter equal to 1/4 of the diameter of the large circle.
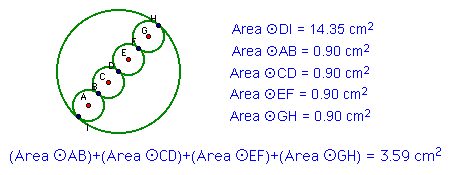 Click
here to view the GSP file to change
the size of the circles (move point I).
Click
here to view the GSP file to change
the size of the circles (move point I).
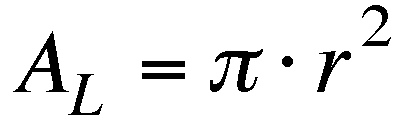
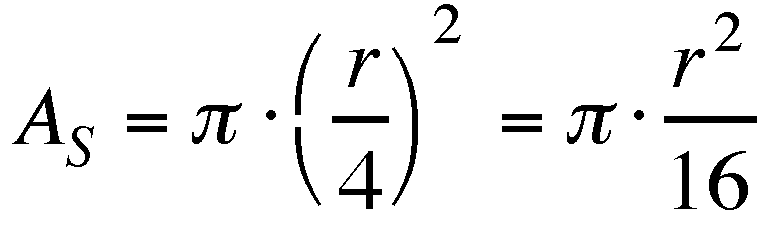
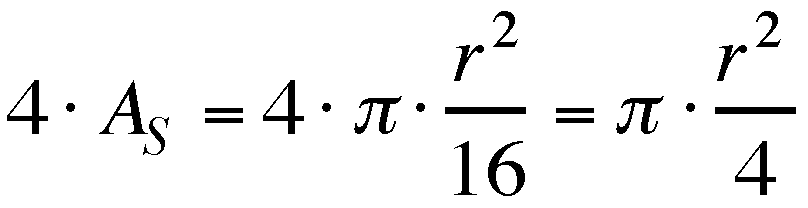
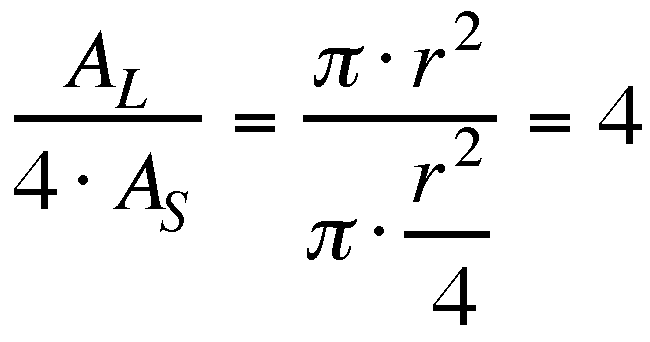 Therefore, our general case has a
tangent circles along the diameter of a larger tangential circle.
The sum of the areas of the smaller circles equals 1/a
times the area of the larger circle.
From the Intermath
site, there is also an extension activity related to this problem
involving the circumferences of the circles.
If you were to walk along the entire
circumferences of all the small circles, would you walk farther
or less far than if you walked around the circumference of the
largest circle? How much more or how much less would you walk?
Therefore, our general case has a
tangent circles along the diameter of a larger tangential circle.
The sum of the areas of the smaller circles equals 1/a
times the area of the larger circle.
From the Intermath
site, there is also an extension activity related to this problem
involving the circumferences of the circles.
If you were to walk along the entire
circumferences of all the small circles, would you walk farther
or less far than if you walked around the circumference of the
largest circle? How much more or how much less would you walk?
 Is the sum of the circumferences of
the smaller tangent circles always equal to the circumference
of the large tangent circle?
I have inserted two spreadsheets so
that we can examine this by looking at several values at one time.
Is the sum of the circumferences of
the smaller tangent circles always equal to the circumference
of the large tangent circle?
I have inserted two spreadsheets so
that we can examine this by looking at several values at one time.
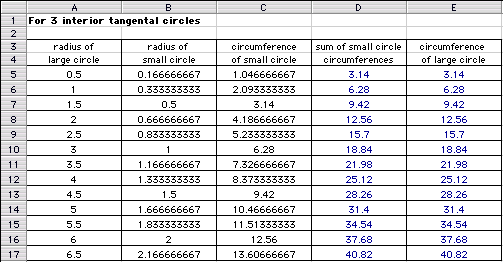
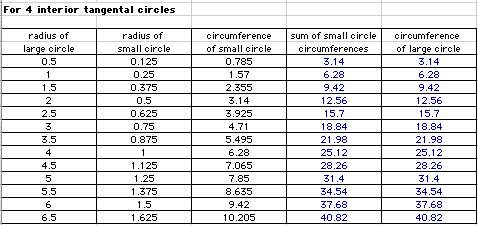 It appears as if the sum of the circumferences
of the small tangential circles is equal to the circumference
of the larger tangential circle. Therefore, you are walking no
further nor no less.
It appears as if the sum of the circumferences
of the small tangential circles is equal to the circumference
of the larger tangential circle. Therefore, you are walking no
further nor no less.
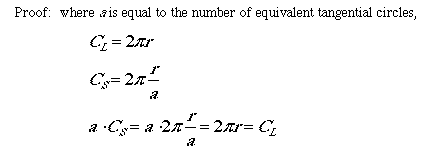
Now, our fun must come to an end. Not to worry,
there are more assignments that will allow us to frolic as we
have done today!
 Just wanted to leave you with another
image of real life tangent circles.
Just wanted to leave you with another
image of real life tangent circles.
Return