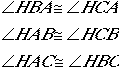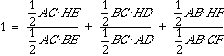Fun with an Acute Triangle,
its Circumcircle, Altitudes, and Intersections
Just when you thought
that it was impossible for me to find more fun in mathematics,
I pull this one out. I know that the title is so exciting that
you can't wait to read all about it, but be patient and try to
take it all in.
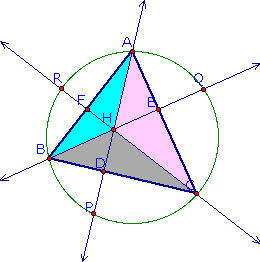
In this investigation,
I am to construct an acute triangle, ABC, and its circumcircle.
Next, the altitudes of the triangles are to be constructed and
extended so that they intersect the circumcircle. Let's go on
and take care of that.
Of course, you can
only see the acute triangle, circumcircle, altitudes, and intersections.
In order to construct the circumcircle, I constructed the perpendicular
bisectors of the triangle and then constructed the circle using
the point of intersection of the perpendicular bisectors as the
center of the circle and a vertex on the triangle as a point on
the circle.
Now, we are ready to
move on to the fun stuff! We want to find:
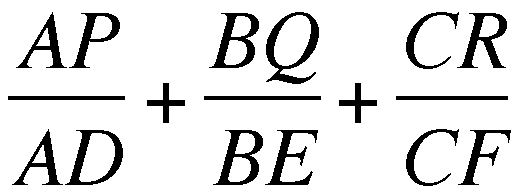
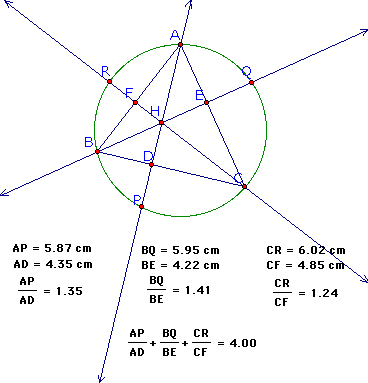
Click here for
a GSP sketch to pull, stretch, shrink, and have fun with to see
if this will always work. Make sure that while you are playing
with this sketch that you see what happens if we had used a right
triangle or an obtuse triangle. You will see why it was important
to start with an acute triangle!
I know that you thought we were having
fun, but the fun is in the proof! Now, we get to prove that this
sum of the ratios is always 4!
Of course, along the way, I have found
something else that is interesting. The segments constructed from
H to the point on the circle are bisected by the side of the triangle
that it passes through. Why you may ask? Let's see if we can figure
it out! Yippee!
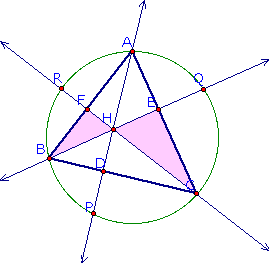In looking at triangles BFH and CEH,
we have similar triangles by Angle-Angle Similarity. Angle BFH
and angle CEH are right angles because the lines constructing
the angles are perpendicular -- remember? We constructed those
lines as altitudes in the beginning. Next, angle BHF and angle
CHE are congruent because they are vertical angles. Therefore,
we will actually have three pairs of similar triangles using the
same argument:
DBFH
~ DCEH
DAFH
~ DCDH
DAEH
~ DBDH
Now, we have a few more sets of congruent
angles that follow from the triangles being similar:
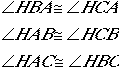It is very important to realize that
angle ABQ and angle ACQ intersect arc AQ, which leads to:
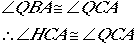Since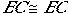 
by the Reflexive Property and 
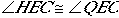because they are both right angles constructed by the original
altitudes, we have congruent triangles by the Angle-Side-Angle
Postulate as shown below.
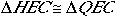
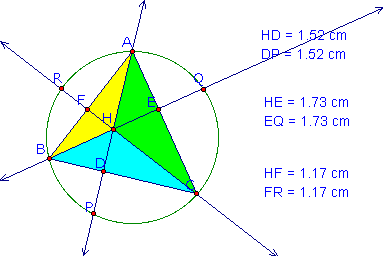
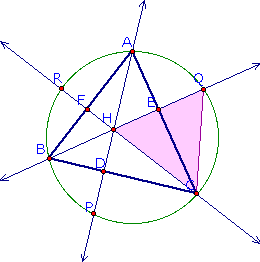Since we now have congruent triangles,
we can use the theorem that states the corresponding parts of
congruent triangles are congruent to prove that HE = EQ, HF =
FR, and HD = DP. Therefore, the segment from H to the point on
the circle is bisected by the side of the triangle that it intersects.
Now, I am going to manipulate some
ratios to see what happens -- remember, our goal is to find
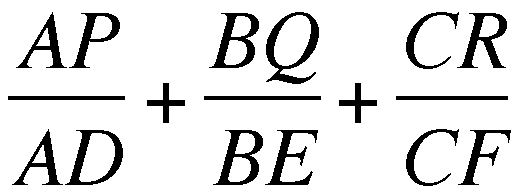First, I am going to look at the first
ratio. Using segment addition and substitution, I get:
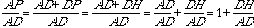Using the same arguments as above leads
to the other ratios:
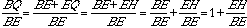
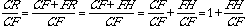This leads to a new ratio of:
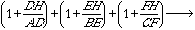
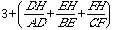From the very beginning of this problem,
we know that the sum of the ratios is 4. That means:
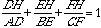I feel that we are getting very close.
Now, I want to look at the areas of three smaller triangles that
would sum to make the area of the larger triangle ABC.
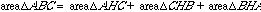If we divide both sides of the equation
by area of triangle ABC, we get:
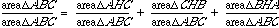
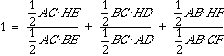
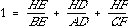This proof is now complete and the
sum of our ratios will always be 4!!!!
Return