The Pedal Point of
a Triangle
(is Not a Pedal at
All - or is it?)
When I think of a pedal,
it is usually as it relates to a bicycle. You can see in this
picture that the man is making his bicycle move by pedaling. Would
the bike move if there was no pedal? Is the pedal necessary? What
would happen if the pedal did not move at all? My questions lead
me to wonder how the pedal point of a triangle moves it. Does
the pedal point move the triangle?
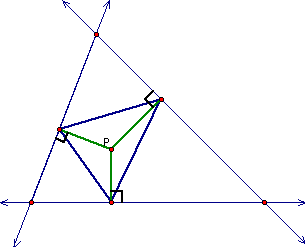
The pedal point of
a triangle is a random point that may lie inside, outside, or
on the triangle. The pedal triangle is then created by constructing
3 lines through the pedal point perpendicular to each side. The
intersections of the perpendicular lines and the sides of the
triangle at the right angle are then connected to form the pedal
triangle.
We are going to look
at various positions of the pedal point in relation to the original
triangle. What happens to our pedal triangle if the point is inside
the original triangle? outside? on? Let's get busy and find out!
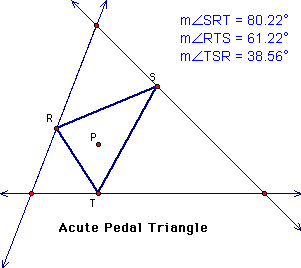
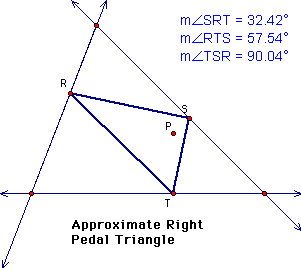
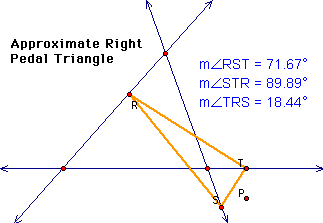
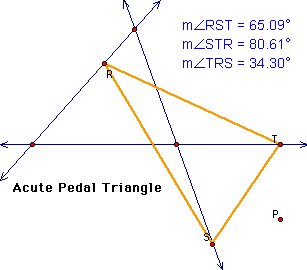
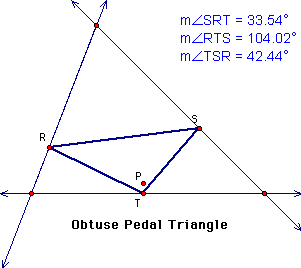It appears as though
the closer the pedal point gets to a side of the original triangle,
the larger the angle in the pedal triangle that P is moving towards.
This allows the pedal triangle to be acute, right, or obtuse within
the original triangle if the pedal point is inside the triangle.
My original triangle was acute. I wonder if this has an effect
on my pedal triangle. Will it be the same for an obtuse or right
triangle?
Click
here to play with the
pedal point, P, of an obtuse triangle.
Click
here to play with pedal
point, P, of a right triangle.
What would happen to
the pedal triangle if the pedal point lay on a vertex of the original
triangle? Would we have an acute triangle, obtuse triangle, or
right triangle? Would we have any triangle at all? It seems like
the pedal point would cause the triangle to collapse if it lies
on a vertex because there cannot be a perpendicular line through
the point and the side at those two sides. Let's see:
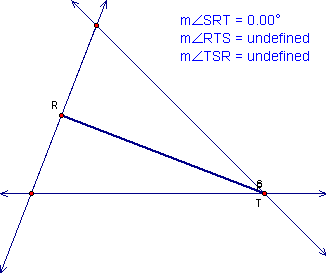How about that?! The
pedal triangle collapses into a line. More importantly than just
a line, it collapses into the altitude from the pedal point vertex
to the opposite side. Very interesting.
What would happen if
we started with an equilateral triangle? Does there exist an equilateral
pedal triangle?
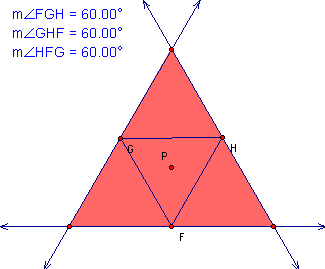Of course it does!
The pedal point of the equilateral triangle is the intersection
of the altitudes. This causes the pedal triangle to be equilateral.
I thought it might be nice to be as creative as the guy who created
this picture:
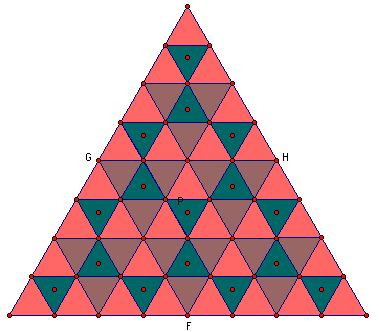This pattern of triangles was generated
by taking the specific pedal point of each equilateral triangle
that lay on the intersection of the altitudes. While it may not
be as creative as the arranged fruit in the still life art above,
it is my best attempt at creativity.
Back to the investigation.
Now, let's look at the pedal triangle in the event that the pedal
point is on the outside of the original triangle.
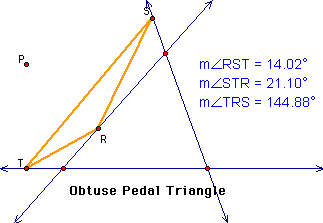
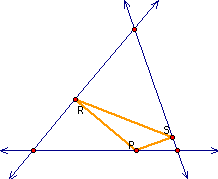
So far, I am not finding
anything that is very interesting. It is interesting that when
the pedal point lies on the original triangle, it is a vertex
of the pedal triangle as shown:
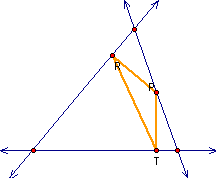
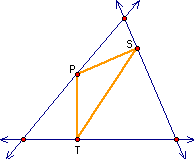The pedal triangles
constructed here are all obtuse. Will it always be obtuse?
So, you can see that the pedal point
does not move the original triangle, but the pedal triangle is
highly dependent on its position - much like the bicycle's position
is dependent on the pedal of the bike.
If you are still interested
in the pedal point and the pedal triangle and their relationship
to the original triangle, here are some other investigations in
which you may look. What if the pedal point is actually the centroid
of the original triangle? incenter? orthocenter? circumcenter?
Return