Find two linear functions f(x) and g(x) such that their product

h(x) = f(x).g(x)

is tangent to each of f(x) and g(x) at two distinct points.

Discuss and illustrate the method and the results.

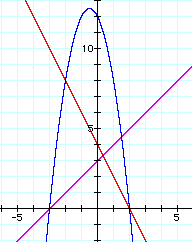
we can write

f(x) = ax + b

as f(x) = a(x - x0)

g(x)= cx + d

as g(x) = c(x - x1)

 

Then h(x) = f(x)g(x) is a parabola which meet with x-axis at x0 and x1.

(because h(x0)=f(x0)g(x0)=a(x0-x0)g(x0)=0 and likewise, h(x1)=0)

Case1) a>0 , c>0

Investigate the case1

We can know that it's impossible for parabola to be tangent to both f(x) and g(x).

 

Case2) a<0 , c<0

Investigate the case2

In this case it's impossible for parabola to be tangent to both f(x) and g(x) as well.

 

Case3) a>0 , c<0

Since

parabola is symmetric against x=x-coordinate of vertex and

h(x) passes through (x0,0) and (x1,0) and

x-coordinate of vertex of h(x)=(x0+x1)/2 and

h(x) must be tagent to each of f(x) and g(x),

the graph must be the following

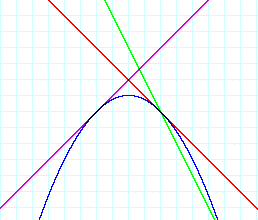
we can get the First Result:

the slope of f(x) = opposite sign of the slope of g(x)

a = -c

 

Let's consider another condition.

 

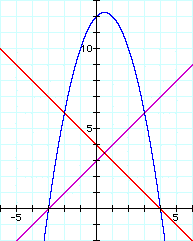
We want to get the y-coordinate of the vertex downward and the make the graph as the following

 

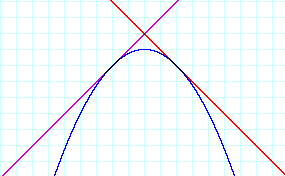
Explore the situation

Note the situation that an intersection of two lines becomes a vertex of their product, parabola.

Let's the vertex (xt, yt). Then h(xt)=f(xt)=g(xt) and h(xt)=f(xt)g(xt)=f(xt)f(xt)=f(xt).

Therfore f(xt)=0 or 1

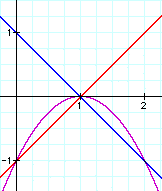
If f(xt)=g(xt)=0 then

x0=x1=xt and f(0)+g(0)=0

Let's see the graph

 

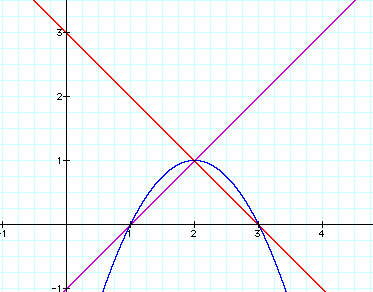
If f(xt)=g(xt)=1 then

f(0)+g(0)=2

Let's see the graph

 

 

Let's see the graphs simultaneously.

 

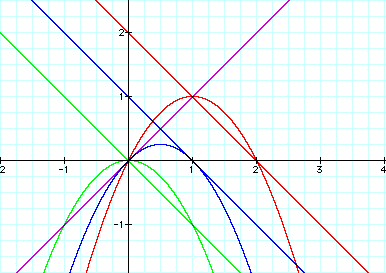
We can realize that the y-value of the parabola which we want to find must be below the product of the y-values of two lines.

To be that situation, two y-values of lines simultaneously must be below "1"and above "0".

we can get the Second Result:

f(0) + g(0) =1

 

RESULT

Two linear functions f(x) and g(x) such that their product

h(x) = f(x).g(x)

is tangent to each of f(x) and g(x) at two distinct points

 

1)the slope of f(x) = opposite sign of the slope of g(x) and

2)f(0) + g(0) =1

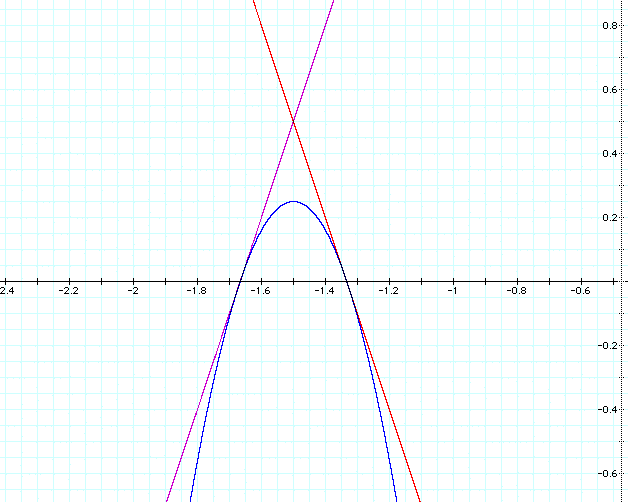
Example 1.

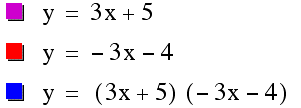
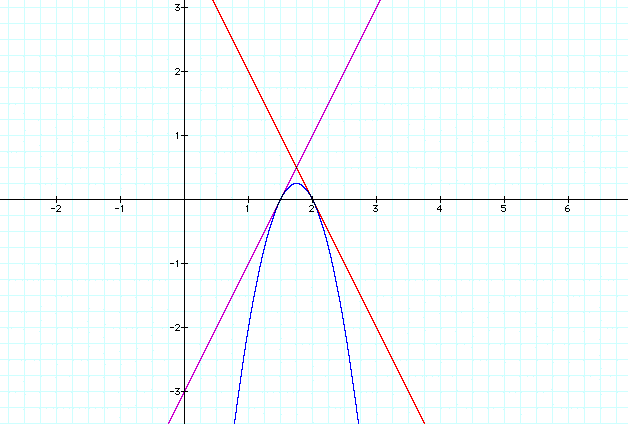
Eample 2.

Return to Hyungsook's homepage