Generate a Fibonnaci sequence in the first column using f(0) = 1, f(1) = 1,

f(n) = f(n-1) + f(n-2)

a. Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence. What happens as n increases? What about the ratio of every second term? etc.

b. Explore sequences where f(0) and f(1) are some arbitrary integers other than 1. If f(0)=1 and f(1) = 3, then your sequence is a Lucas Sequence. All such sequences, however, have the same limit of the ratio of successive terms.

Fibonnaci Sequence

n f(0)=1, f(1)=1 Ratio=f(n)/f(n-1) f(0)=3, f(1)=4 Ratio=f(n)/f(n-1)
0 1 3
1 1 1 4 1.33333333333333
2 2 2 7 1.75
3 3 1.5 11 1.57142857142857
4 5 1.66666666666667 18 1.63636363636364
5 8 1.6 29 1.61111111111111
6 13 1.625 47 1.62068965517241
7 21 1.61538461538462 76 1.61702127659574
8 34 1.61904761904762 123 1.61842105263158
9 55 1.61764705882353 199 1.61788617886179
10 89 1.61818181818182 322 1.61809045226131
11 144 1.61797752808989 521 1.61801242236025
12 233 1.61805555555556 843 1.61804222648752
13 377 1.61802575107296 1364 1.61803084223013
14 610 1.61803713527851 2207 1.61803519061584
15 987 1.61803278688525 3571 1.6180335296783
16 1597 1.61803444782168 5778 1.61803416409969
17 2584 1.61803381340013 9349 1.61803392177224
18 4181 1.61803405572755 15127 1.61803401433308
19 6765 1.61803396316671 24476 1.61803397897799
20 10946 1.6180339985218 39603 1.61803399248243
21 17711 1.61803398501736 64079 1.61803398732419
22 28657 1.6180339901756 103682 1.61803398929446

From the table above we can see that two fibonnaci sequences with different starting points converge to the same point in the ratio of each pair of adjacent terms.

Of course, the ratio does not increase as n inreases but it goes towards a particular value.

What is a value of the ratio?

we can notice the value is a golden ratio.

Golden Ratio

Given segment, we can think the point that s: t is the same to s+t:s. we call the ratio golden ratio(=Phi=1.618033...)

Let's try to find the value.

s : t = s+t : s

Divide by t , then

s / t : 1 = (s+t) / t : s / t

Let s / t = r

r : 1 = r + 1 : r

r^2 - r - 1 = 0

By quadratic formula and since r is positive

r = (1 + sqrt(5) ) / 2 = 1.618033...

Also , we can get the value from the following formuli

and

sqrt(1 + sqrt(1 + sqrt(1 + sqrt(1 + .....) ) ) )

Why are the values(=x's) above same to r ?

x = 1 + 1 / x or x = sqrt(1 + x)

These equations result in x^2 - x - 1 = 0. Therefore x = r

 

Lucas Sequence

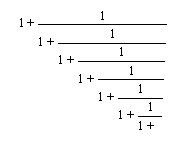
n f(0)=1, f(1)=3 Ratio=f(n)/f(n-1)
0 1
1 3 3
2 4 1.33333333333333
3 7 1.75
4 11 1.57142857142857
5 18 1.63636363636364
6 29 1.61111111111111
7 47 1.62068965517241
8 76 1.61702127659574
9 123 1.61842105263158
10 199 1.61788617886179
11 322 1.61809045226131
12 521 1.61801242236025
13 843 1.61804222648752
14 1364 1.61803084223013
15 2207 1.61803519061584
16 3571 1.6180335296783
17 5778 1.61803416409969
18 9349 1.61803392177224
19 15127 1.61803401433308
20 24476 1.61803397897799
21 39603 1.61803399248243
22 64079 1.61803398732419

We can also find that lucas sequence converges to the golden ratio

Return to Hyungsook's homepage