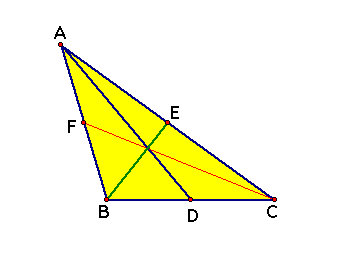
Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find.

Let's construct the triangle with the three sides having the lengths of the three medians from given triangle

I will make a second triangle with CF as a side from given triangle.

Step 1: Construct a line passing through F parallel to BE

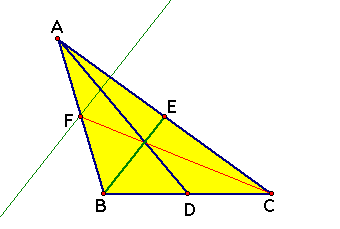
Step 2: Construct a line passing through F parallel to AB

Step 3: Let's call the intesection as G. Then BEGF is to be a parallelogram and BE=FG.

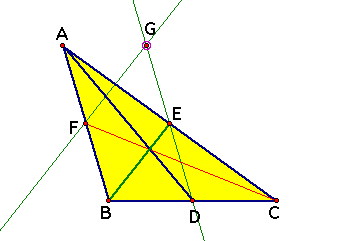
Step 4: Construct a segment passing through C and G

 

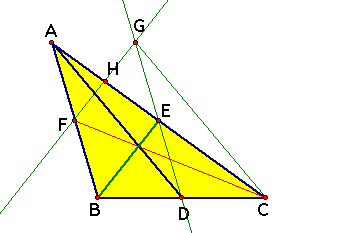
Why is a length of GC going to be the same to the one of AD?

 

What is E in the triangle CFG? ------ E is a centroid of CFG

1) AFH is similar to ABE and the ratio is 1:2

2) 2FH=BE and FG=BE(Step 3) therefore H is a midpoint of FG, i.e CH is a median of CFG

3) AH=HE and AE=EC therefore E is the point which is to be a 2:1 of from C to H, i.e E is a centroid

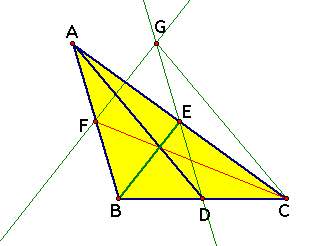
Investigate that ADCG is to be parallelogram and consider the reason

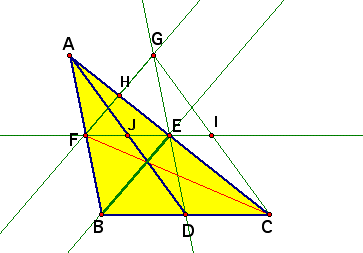
Why is ADCG a parallelogram?

1) FE=2EI and J is midpoint of EF and FE=DC therefore FE=JI and JI=DC

2) FE is parallel to DC therefore JDCI is parallelogram

3) AD=2JD and GC=2IC therefore AD=GC

 

What is the relationship between triangle ABC and triangle CFG?

Consider triangle ABE and triangle AFH.

They are similar with the ratio 2:1. So BE=2FH and AreaABE = 4 AreaAFH.

Area ABC = 2 Area ABE = 2Area AFC and so Area ABE = Area AFC

Area CFH = Area AFC - Area AFH = Area ABE - 1/4 Area ABE = 3/4 Area ABE

 

Since Area ABC = 2 Area ABE and Area CFG = 2 Area CFH,

 

Our Result

Area CFG = 3/4 Area ABC

 

Do the various shapes of triangles satisfy the above relation?

What relationship is there between first triangle and second?

 

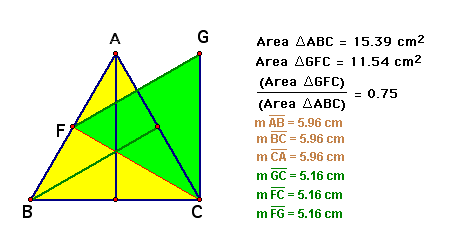
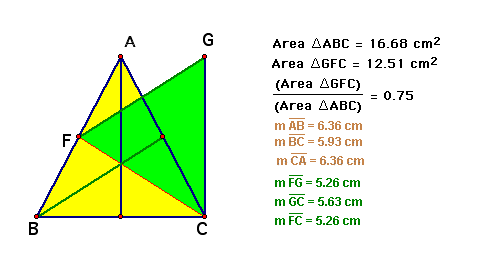
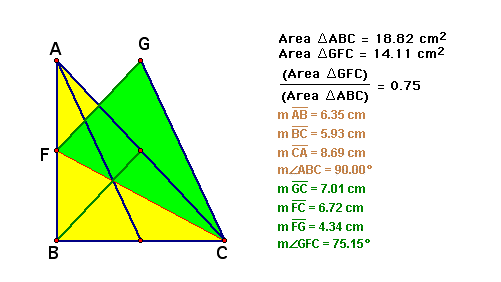
Let's try to make sure by using measure in GSP for many cases.

Case 1. Equilateral triangl

If first triangle is equilateral then second trangle is also equilateral

 

Case 2. Isosceles triangle

If first triangle is isosceles then second trangle is also isosceles

Case 3. Right triangle

Even though first triangle is rihgt, second trangle does not have to be a right

Investigate the condition that the first triangle make the second one to be a right

 

Return to Hyungsook's homepage