Intermath: Investigations: Algebra: Graphs
Take any equation and graph both sides of the equation. For example, if you are trying to solve the equation 3x - 4 = 11, graph y1 = 3x - 4 and graph y2 = 11. How can you identify the solution to the equation on the graph?
The statement of equality is the important key to answering this question. The equals sign is not a production function; it is representing a relationship between each side of the equation. That relationship says that both sides are equal to each other. Because there is a relationship between each side, it will be represented on a graph.
The next important factor in answering this question would be, what happens on a graph when both sides of the equation are equal. It is n ot surprising what happens in this instance. If there are two lines each representing one side of an equation, then those two lines will intersect where the equation is true. In some cases, the equation will always be true, and the lines will overlap. In the case of exponents, there may be multiple intersections where the equation will be true.
Let's take a few examples.
First, lets try the given example.
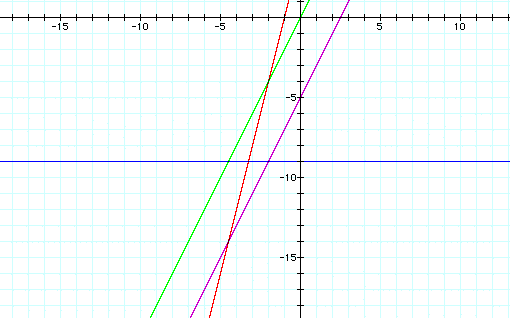
2x-5 is purple
4+4x is red
-9 is blue
2x is green

Note that in this example y=11 and y=3x-4. It is given that at the intersection y=11, because we already knew that at the start. However, we did not know what x was equal to, but if we trace the intersection point down to the x axis, it crosses where x=5. This is what we have discovered from this graph. When x=5 and y=11, the equation y=3x-4 is true!
Now let's try an exponent like x^2=y, where y=4.
x^2 is purple
4 is red
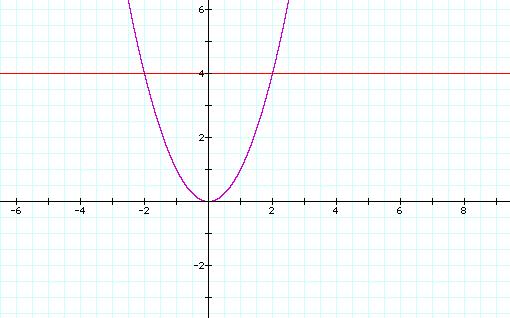
Note in this example that there are two points where the lines intersect. Both points are along the line y=4, but there are two points that x can equal to make the equation true. Tracing down from the intersection to the x axis, the first point is x=-2. Tracing down from the right point to the x axis, the second point is x=2.
One final example, 2x-5=4+4x. In this equation, y=2x-5 (purple) and y=4+4x (red). (This equation could be simplified algebraically to -9=2x. We will look at both of these. y=-9 (blue) & y=2x (green))
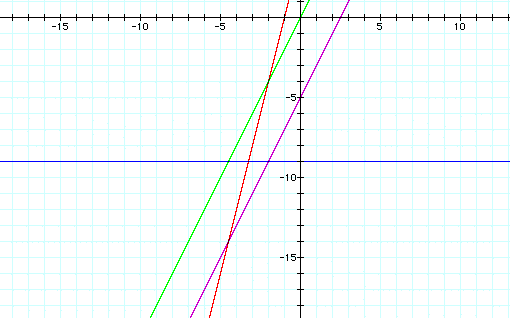
Note that the intersections that should be considered are between the green & blue, and the red & purple. This example shows not only the equality of two functions, but also equality of two seperate equalities. The green and the blue intersection can be traced to show that they intersect at x=-4.5, and the same for the red & purple intersection. That shows that both the equations are true for 4.5=x.