Intermath: Investigations: Geometry: Quadrilaterials
Given a triangle, how do you construct a square with the same area using a dynamic geometry software?
(To do this, it requires some knowledge of the working of a dynamic geometry software, such as Geometer's Sketch Pad, the one used in this example.)
First, the given triangle must be constructed. One way to do that in GSP, is to create three points on the page. Highlight those points and under the construct dropbox select "segements". These three points will be turned into a triangle by adding the segements that now exist between them. The two steps will look like this:

Next, because of the incredible features of this software it is possible to measure the area created by the triangle. By selecting the three points on the triangle, a triangle interior would be created. Highlighting the triangle interior and looking under the Measure drop, select area. This selection puts the dyanmic mearsurement of the area on the screen. (Note on the demonstration that the area adjusts as any of the points are moved to create a new triange area.)
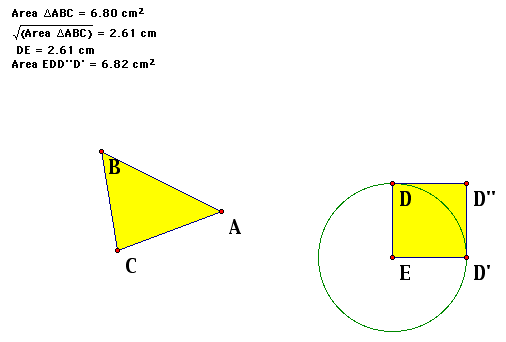
The following is not concerned with procedure, it is based on logic and understanding. Say, for instance, that the triangle's area is 9 cm^2 (for simplicity). If we were seeking to create a square with the same measure, then the following is known. The area of a square is given by A^2=area, where A is the length of one side of the square. One knows that the area=9 cm^2, and so A^2=9 cm^2. Therefore A is equal to the squareroot of 9 cm^2, which equals 3 cm. With this knowledge, one can construct a square with side lengths 3 cm.
This is done by first constructing a circle. Using the center point and the provided point on the circle, construct a segment. Marking the center point as the center for rotation, the segment and its point can be rotated 90 degrees about the center to create a second leg of the square. By marking the length of one of the sides as a vector, the other side can be translated that length. This leaves only one side to create, which can be done by selecting the two points and creating that segment. The measure of any of the sides can be taken by highlighting two points connecting a side and under the Measure drop, selecting distance. Move the point creating a longer or shorter segment until it matches the squareroot of the triangles area. (The circle can be hidden after the construction is complete.)